探月飞船进入地月转移轨道后关闭推进器,会依靠惯性沿地球与月球的连心线飞往月球。在飞行途中飞船中会经过一个特殊的点P,在这一点飞船所受到的地球对它的引力与月球对它的引力正好抵消(不考虑其他星体对飞船的引力作用)已知地球质量为M1,月球质量为M2,地球中心与月球中心之间的距离为 r.
(1)试分析在探月飞船靠惯性飞行到达P点的过程中,飞船的动能如何变化?飞船的加速度如何变化?
(2)P点距离地球中心多远?
如图所示,小球被轻质细绳系住斜吊着放在静止的光滑斜面上,设小球质量m=1kg,斜面倾角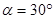 ,悬线与竖直方向夹角
,悬线与竖直方向夹角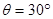 ,光滑斜面的质量为3kg,置于粗糙水平面上.g=10m/s2.求:
,光滑斜面的质量为3kg,置于粗糙水平面上.g=10m/s2.求:
悬线对小球拉力大小.
地面对斜面的摩擦力的大小和方向.
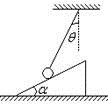
如图所示,半径为R的半球支撑面顶部有一小孔. 质量分别为m1和m2的两只小球(视为质点),通过一根穿过半球顶部小孔的细线相连,不计所有摩擦. 请你分析m2小球静止在球面上时,其平衡位置与半球面的球心连线跟水平方向的夹角为θ,则m1、m2、θ和R之间应满足什么关系;
若m2小球静止于θ=45°处,现将其沿半球面稍稍向下移动一些,则释放后m2能否回到原来位置?请作简析。

在粗糙的水平面上放一物体A,A上再放一质量为m的物体B,AB间的动摩擦因数为 ,施加一水平力F与A,计算下列情况下A对B的摩擦力的大小
,施加一水平力F与A,计算下列情况下A对B的摩擦力的大小
⑴当AB一起做匀速运动时
⑵当AB一起以加速度a向右做匀加速运动时
⑶当力F足够大而使AB发生相对运动时
如下图所示,高为0.45m的光滑水平桌面上的物体m1=2kg,以水平速度υ1=5m/s向右运动,与静止的另一物体m2=lkg相撞,若碰
撞后m1仍向右运动,速度变为υ/1=3m/s,求:
(1)m2落地时距桌边缘A点的水平距离。
(2)m2落地时动量的大小。(不计空气阻力g=l0m/s2)
如图所示,有一电子束从a点处以一定的水平速度飞向竖直放置的荧光屏,并垂直击中荧光屏上的b点.已知电子的质量为m,电量为e.
若在电子束运行途中加一个仅存在于半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里,圆心O在点a、b连线上,点O距荧光屏的距离为L。
(1)为使电子束仍击中荧光屏上的点b,可加一场强为E的匀强电场.指出此匀强电场的方向和范围,并求出电子束的速度。
(2)现撤去电场,电子束仍以原速度大小沿水平方向从a点发射,试求出此时侧移量y
的表达式。