已知 ,过
,过 的直线与
的直线与 轴和
轴和 轴分别交于
轴分别交于 两点,若
两点,若 恰为线段
恰为线段 的中点,求
的中点,求 两点的坐标.
两点的坐标.
已知 ,当k为何值时.
,当k为何值时.
(1)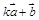 与
与 垂直;
垂直;
(2)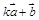 与
与 平行,平行时它们是同向还是反向.
平行,平行时它们是同向还是反向.
已知抛物线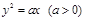 ,直线l与抛物线交于A、B,且
,直线l与抛物线交于A、B,且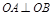 ,点
,点 在AB上,又
在AB上,又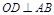 .
.
(1)求直线l的方程;
(2)求a的值;
(3)求△OAB的面积.
如图,在棱长是1的正方体ABCD-A1B1C1D1中,点E,F,G分别是DD1,BD,BB1的中点. 
(1)求证:EF⊥CF;
(2)求EF与CG所成的角的余弦值;
(3)求三棱锥G-CEF的体积.
已知椭圆C: ,点M(2,1).
,点M(2,1).
(1)求椭圆C的焦点坐标和离心率;
(2)求通过M点且被这点平分的弦所在的直线方程.
已知点A(-1,0),B(1,0),直线AM,BM相交于点M,且它们的斜率之积是2,求点M的轨迹方程,并指出该轨迹曲线的离心率.