在△ABC中,角A,B,C的对边分别为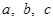 ,且A,B,C成等差数列。
,且A,B,C成等差数列。
(1)若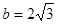 ,
,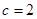 ,求△ABC的面积;
,求△ABC的面积;
(2)若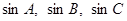 成等比数列,试判断△ABC的形状。
成等比数列,试判断△ABC的形状。
若不等式组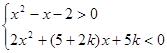 的解集中所含的整数解只有-2,求k取值范围
的解集中所含的整数解只有-2,求k取值范围
(本小题满分15分)如图,已知抛物线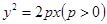 上点
上点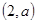 到焦点
到焦点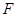 的距离为3,直线
的距离为3,直线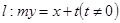 交抛物线
交抛物线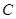 于
于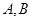 两点,且满足
两点,且满足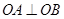 。圆
。圆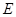 是以
是以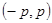 为圆心,
为圆心,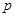 为直径的圆.
为直径的圆.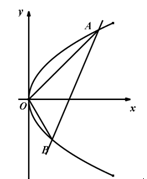
(1)求抛物线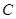 和圆
和圆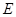 的方程;
的方程;
(2)设点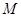 为圆
为圆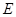 上的任意一动点,求当动点
上的任意一动点,求当动点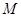 到直线
到直线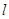 的距离最大时的直线方程.
的距离最大时的直线方程.
(本小题满分15分)已知函数 是定义在
是定义在 上的偶函数,
上的偶函数, ,其中
,其中 均为常数.
均为常数.
(1)求实数 的值;
的值;
(2)试讨论函数 的奇偶性;
的奇偶性;
(3)若 ,求函数
,求函数 的最小值.
的最小值.
(本小题满分14分))如图,在三棱柱 中,
中, ⊥底面
⊥底面 ,且△
,且△ 为正三角形,
为正三角形, ,
, 为
为 的中点.
的中点.
(1)求证:直线 ∥平面
∥平面 ;
;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(3)求三棱锥 的体积.
的体积.