从原点出发的某质点M,按向量a=(0,1)移动的概率为 ,按向量b=(0,2)移动的概率为
,按向量b=(0,2)移动的概率为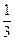 ,设M可到达点(0,n)的概率为Pn
,设M可到达点(0,n)的概率为Pn
(1)求P1和P2的值;(2)求证: =
=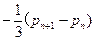 ;(3)求
;(3)求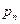 的表达式。
的表达式。
已知椭圆的一个焦点 ,对应的准线方程为
,对应的准线方程为 ,且离心率e满足
,且离心率e满足 ,e,
,e,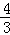 成等比数列.
成等比数列.
(1)求椭圆的方程;
(2)试问是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线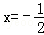 平分?若存在,求出l的倾斜角的取值范围;若不存在,请说明理由.
平分?若存在,求出l的倾斜角的取值范围;若不存在,请说明理由.
已知一圆经过点A(2,﹣3)和B(﹣2,﹣5),且圆心C在直线l:x﹣2y﹣3=0上,求此圆的标准方程.
在数列{an}中,已知a1=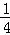 ,
, ,bn+2=3
,bn+2=3 an(n∈N*).
an(n∈N*).
(1)求数列{an}、{bn}的通项公式;
(2)设数列{cn}满足cn=an•bn,求{cn}的前n项和Sn.
如图,正方体ABCD﹣A1B1C1D1中,E为AB中点,F为正方形BCC1B1的中心.
(1)求直线EF与平面ABCD所成角的正切值;
(2)求异面直线A1C与EF所成角的余弦值.
甲、乙两校各有3名教师报名支教,期中甲校2男1女,乙校1男2女.
(Ⅰ)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(Ⅱ)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.