过点T(2,0)的直线 交抛物线y2=4x于A、B两点.
交抛物线y2=4x于A、B两点.
(I)若直线l交y轴于点M,且 当m变化时,求
当m变化时,求 的值;
的值;
(II)设A、B在直线 上的射影为D、E,连结AE、BD相交于一点N,则当m变化时,点N为定点的充要条件是n=-2.
上的射影为D、E,连结AE、BD相交于一点N,则当m变化时,点N为定点的充要条件是n=-2.
已知抛物线C:y=-x2+mx-1和点A(3,0),B(0,3),求抛物线C与线段AB有两个不同交点的充要条件。
已知数列{an}、{bn}满足:bn= ,求证:数列{an}成等差数列的充要条件是数列{bn}也是等差数列。
,求证:数列{an}成等差数列的充要条件是数列{bn}也是等差数列。
如图,点A、B、C都在函数y= 的图像上,它们的横坐标分别是a、a+1、a+2
的图像上,它们的横坐标分别是a、a+1、a+2 又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a).
又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a).
(1)求函数f(a)和g(a)的表达式;
(2)比较f(a)与g(a)的大小,并证明你的结论.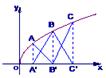
对函数y=f(x)定义域中任一个x的值均有f(x+a)=f(a-x),
(1)求证y=f(x)的图像关于直线x=a对称;
(2)若函数f(x)对一切实数x都有f(x+2)=f(2-x),且方程f(x)=0恰好有四个不同实根,求这些实根之和。
已知函数f(x)=ax3+bx2+cx+d的图像如图,求b的范围.