在极坐标系中,已知圆C的圆心坐标为(3, ),半径为1,点Q在圆C上运动,O为极点。
),半径为1,点Q在圆C上运动,O为极点。
(1)求圆C的极坐标方程;
(2)若点 在直线OQ上运动,且满足
在直线OQ上运动,且满足 ,求动点P的轨迹方程。
,求动点P的轨迹方程。
设函数 .
.
(Ⅰ)若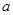 是从-2、-1、0、1、2五个数中任取的一个数,
是从-2、-1、0、1、2五个数中任取的一个数, 是从0、1、2三个数中任取的一个数,求函数
是从0、1、2三个数中任取的一个数,求函数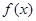 无零点的概率;
无零点的概率;
(Ⅱ)若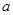 是从区间[-2,2]任取的一个数,
是从区间[-2,2]任取的一个数, 是从区间[0,2]任取的一个数,求函数
是从区间[0,2]任取的一个数,求函数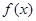 无零点的概率.
无零点的概率.
如图是一个计算 个数
个数 的和的程序框图,请完成该图的程序框:
的和的程序框图,请完成该图的程序框:
(I)请在图中判断框内(1)处和执行框中的(2)处填上合适的语句,使之能完成该题算法功能;
(II)根据程序框图写出程序.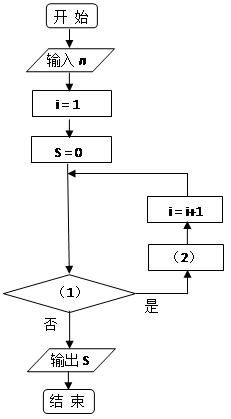
下面有两个关于“袋子中装有红、白两种颜色的相同小球,从袋中无放回地取球”的游戏规则,这两个游戏规则公平吗?为什么?
| 游 戏 1 |
游 戏 2 |
| 2个红球和2个白球 |
3个红球和1个白球 |
| 取1个球,再取1个球 |
取1个球,再取1个球 |
| 取出的两个球同色→甲胜 |
取出的两个球同色→甲胜 |
| 取出的两个球不同色→乙胜 |
取出的两个球不同色→乙胜 |
从某小学随机抽取100名学生,将他们的身高(单位:厘米)按照区间 [ 100 , 110),[ 110 , 120),[ 120 , 130),[130 ,140) , [140 , 150]进行分组,得到频率分布直方图(如图).
(Ⅰ)求直方图中a的值;
(Ⅱ)若要从身高在[ 120 , 130),[130 ,140) , [140 , 150] 三组内的学生中,用分层抽样的方法选取18人参加一项活动,求从身高在[140 ,150]内的学生中应选取的人数;
(Ⅲ)这100名学生的平均身高约为多少厘米?
选修4-5:不等式选讲
关于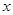 的不等式
的不等式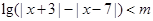 .
.
(1)当 时,解此不等式;
时,解此不等式;
(2)设函数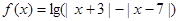 ,当
,当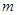 为何值时,
为何值时, 恒成立?
恒成立?