已知点 ,点
,点 为直线
为直线 上的一个动点.
上的一个动点.
(1)求证: 恒为锐角;
恒为锐角;
(2)若四边形 为菱形,求
为菱形,求 的值.
的值.
已知函数 .
.
(1)请用“五点法”画出函数 在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);

(2)求函数 的单调递增区间;
的单调递增区间;
(3)当 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的 的值.
的值.
已知函数 ,其中
,其中 为常数.
为常数.
(1)若函数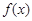 在区间
在区间 上单调,求
上单调,求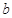 的取值范围;
的取值范围;
(2)若对任意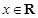 ,都有
,都有 成立,且函数
成立,且函数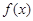 的图象经过点
的图象经过点 ,
,
求 的值.
的值.
抛物线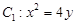 在点
在点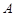 ,
, 处的切线垂直相交于点
处的切线垂直相交于点 ,直线
,直线 与椭圆
与椭圆 相交于
相交于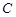 ,
, 两点.
两点.
(1)求抛物线 的焦点
的焦点 与椭圆
与椭圆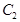 的左焦点
的左焦点 的距离;
的距离;
(2)设点 到直线
到直线 的距离为
的距离为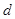 ,试问:是否存在直线
,试问:是否存在直线 ,使得
,使得 ,
,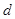 ,
, 成等比数列?若存在,求直线
成等比数列?若存在,求直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
设函数 .
.
(1)求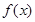 的单调区间;
的单调区间;
(2)设函数 ,若当
,若当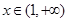 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.