已知正方形的中心为直线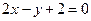 和
和 的交点,正方形一边所在直线的方程为
的交点,正方形一边所在直线的方程为 ,求其他三边所在直线的方程.
,求其他三边所在直线的方程.
某跨国饮料公司对全世界所有人均GDP(即人均纯收入)在0.5-8千美元的地区销售该公司A饮料的情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减。
(Ⅰ)下列几个模拟函数中(x表示人均GDP,单位:千美元,y表示年人均A饮料的销量,单位;升),用哪个来描述人均A饮料销量与地区的人均GDP的关系更合适?说明理由。
① ,②
,② ,③
,③ ,④
,④
(Ⅱ)若人均GDP为1千美元时,年人均A饮料的销量为2升;若人均GDP为4千美元时,年人均A饮料的销量为5升,把(Ⅰ)中你所选的模拟函数求出来,并求在各个地区中,年人均A饮料的销量最多是多少?
(Ⅲ)因为A饮料在B国被检测出杀虫剂的含量超标,受此事件的影响,A饮料在人均GDP低于3千美元和高于6千美元的地区销量下降5%,其它地区的销量下降10%,根据(Ⅱ)所求出的模拟函数,求在各个地区中,年人均A饮料的销量最多为多少?
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,G是CC1上的动点。
(Ⅰ)求证:平面ADG⊥平面CDD1C1
(Ⅱ)判断B1C1与平面ADG的位置关系,并给出证明;
(Ⅲ)若G是CC1的中点,求二面角G-AD-C的大小。
在△ 中,已知a、b、c分别是三内角
中,已知a、b、c分别是三内角 、
、 、
、 所对应的边长,且
所对应的边长,且
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,试判断△ABC的形状并求角
,试判断△ABC的形状并求角 的大小.
的大小.
在平面直角坐标系上,设不等式组 (
( )
)
所表示的平面区域为 ,记
,记 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为 .
.
(Ⅰ)求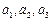 并猜想
并猜想 的表达式再用数学归纳法加以证明;
的表达式再用数学归纳法加以证明;
(Ⅱ)设数列 的前
的前 项和为
项和为 ,数列
,数列 的前
的前 项和
项和 ,是否存在自然数m?使得对一切
,是否存在自然数m?使得对一切 ,
, 恒成立。若存在,求出m的值,若不存在,请说明理由。
恒成立。若存在,求出m的值,若不存在,请说明理由。
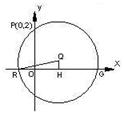
设圆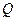 过点P(0,2), 且在
过点P(0,2), 且在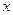 轴上截得的弦RG的长为4.
轴上截得的弦RG的长为4.
(1)求圆心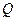 的轨迹E的方程;
的轨迹E的方程;
(2)过点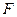 (0,1),作轨迹
(0,1),作轨迹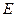 的两条互相垂直的弦
的两条互相垂直的弦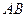 、
、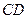 ,设
,设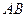 、
、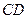 的中点分别为
的中点分别为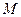 、
、 ,试判断直线
,试判断直线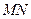 是否过定点?并说明理由.
是否过定点?并说明理由.