地面上有两座塔AB、CD,相距120米,一人分别在两塔底部测得一塔顶仰角为另一塔顶仰角的2倍,在两塔底连线的中点O测得两塔顶的仰角互为余角,求两座塔的高度。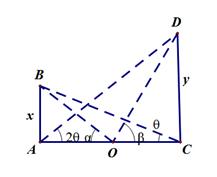
(本小题满分12分)
已知M(-3,0)﹑N(3,0),P为坐标平面上的动点,且直线PM与直线PN的斜率之积为常数m(m -1,m
-1,m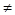 0).
0).
(1)求P点的轨迹方程并讨论轨迹是什么曲线?
(2)若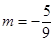 , P点的轨迹为曲线C,过点Q(2,0)斜率为
, P点的轨迹为曲线C,过点Q(2,0)斜率为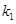 的直线
的直线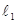 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为 ,求证
,求证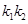 为定值;
为定值;
(3)在(2)的条件下,设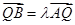 ,且
,且 ,求
,求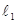 在y轴上的截距的变化范围.
在y轴上的截距的变化范围.
.(本小题满分12分)
如图5所示的多面体是由底面为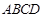 的长方体被截面
的长方体被截面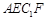 所截
所截
而得到的,其中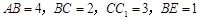 .
.
(1)求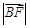 ;
;
(2)求点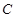 到平面
到平面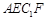 的距离.
的距离.
(本小题满分10分)
已知p:≤2,q:x2-2x+1-m2≤0(m>0),若非p是非q的必要不充分条件,求实数m的取值范围.
(本小题满分12分)
已知x,y之间的一组数据如下表:
(1)分别从集合A={1,3,6,7,8},
B={1,2,3,4,5}中各取一个数x,y,求x+y≥10的概率;
(2)对于表中数据,甲、乙两同学给出的拟合直线分别为y=x+1与y=x+,试根据残差平方和:(yi-i)2的大小,判断哪条直线拟合程度更好.
(本小题满分12分)
已知定义域为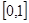 的函数
的函数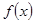 同时满足以下三个条件:
同时满足以下三个条件:
①对任意的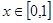 ,总有
,总有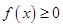 ;
;
②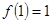 ;
;
③若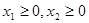 且
且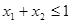 ,则有
,则有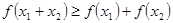 成立,则称
成立,则称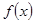 为“友谊函数”。
为“友谊函数”。
(1)若已知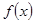 为“友谊函数”,求
为“友谊函数”,求 的值;
的值;
(2)函数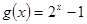 在区间
在区间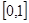 上是否为“友谊函数”?并给出理由;
上是否为“友谊函数”?并给出理由;
(3)已知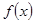 为“友谊函数”,且
为“友谊函数”,且 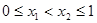 ,求证:
,求证: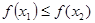 。
。