如图16-44所示,初速度为零,所带电量为q的离子经过电压为U的电场加速后进入磁感强度为B的匀强磁场中,沿半圆周运动而达到记录它的照相底片P上,测得它在P上的位置到入口处的距离为d,求该离子的质量。
两平行金属板竖直放置,距离为d.把它们分别与电压为U的直流电源两极相连,如图所示.一个质量为m、电荷量为q的带电微粒位于两金属板上端的中点处,无初速释放,最后落在某一金属板上,微粒到达该金属板时的动能为Ek.现保持其他条件不变,使电压U加倍,问满足怎样的条件,微粒到达该金属板时的动能仍为Ek?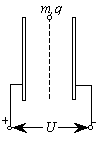
在水平向右的匀强电场中,置一光滑导轨,轨道由水平部分和与之相连接的半圆环ABC组成,半圆环半径为R,A为最低点,C为最高点.如图,今距A点为L的O处有一质量为m,带正电荷的小球,从静止开始沿水平部分进入圆环.若Eq=mg(q代表小球电荷量),则L必须满足什么条件才能使小球在半圆环上运动时,不脱离圆环.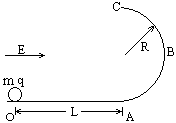
如图所示,质量为m、电荷量为+q的物体,可视为质点.可以在倾角为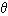 的足够长的斜面上运动,斜面最下端有一个与斜面垂直的挡板OP,物体运动所到之处都处于水平向左的匀强电场中,匀强电场场强为E,开始时物体停在斜面上比底面高h的位置上,因受到一沿斜面向上的瞬时冲量I0的作用而开始沿斜面向上运动,物体与斜面间的动摩擦因数μ=tg
的足够长的斜面上运动,斜面最下端有一个与斜面垂直的挡板OP,物体运动所到之处都处于水平向左的匀强电场中,匀强电场场强为E,开始时物体停在斜面上比底面高h的位置上,因受到一沿斜面向上的瞬时冲量I0的作用而开始沿斜面向上运动,物体与斜面间的动摩擦因数μ=tg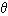 ,物体与挡板碰撞时机械能损失不计,物体所带电量始终不变,求开始运动到停止运动所通过的总路程S为多少?
,物体与挡板碰撞时机械能损失不计,物体所带电量始终不变,求开始运动到停止运动所通过的总路程S为多少?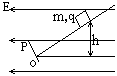
如图是静电分选器的原理示意图,将磷酸盐和石英的混合颗粒由传送带送至两个竖直的带电平行板上方,颗粒经漏斗从电场区域中央处开始下落.经分选后的颗粒分别装入A.B桶中.混合颗粒离开漏斗进入电场时磷酸盐颗粒带正电,石英颗粒带负电,所有颗粒所带的电量与质量之比均为10–5C/kg.若已知两板间的距离为10cm,颗粒在电场中下落的竖直高度为50cm.设颗粒进入电场时的初速度为零,颗粒间的相互作用力不计.如果要求两种颗粒离开两极板间的电场区域时不接触到极板而且有最大的偏转量.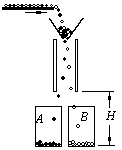
(1)两极板间所加的电压.
(2)若带电平行板的下端距A.B桶底的高度为H=1.0m,求颗粒落至桶底时的速度大小
如图所示,一根对称的A形玻璃管置于竖直平面内,管所在的空间有E=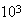 V/m、方向向下的匀强电场,重力G=1.0×
V/m、方向向下的匀强电场,重力G=1.0× N,电荷量为-2.0×
N,电荷量为-2.0×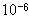 C的小物体m在管内从A点由静止开始运动,m与管壁的动摩擦因数为0.5,管长AB=BC=2m,管的B处为一极短的光滑圆弧,管AB、BC与水平方向的夹角均为37°,(g取10m/
C的小物体m在管内从A点由静止开始运动,m与管壁的动摩擦因数为0.5,管长AB=BC=2m,管的B处为一极短的光滑圆弧,管AB、BC与水平方向的夹角均为37°,(g取10m/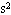 ) 问:
) 问: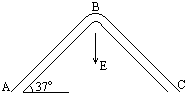
(1)m达到最高点时的速度多大?
(2)m从A点开始运动到第一次速度为零的位置在何处?
(3)从A开始运动,到最终停下来总路程为多大?