如图是静电分选器的原理示意图，将磷酸盐和石英的混合颗粒由传送带送至两个竖直的带电平行板上方，颗粒经漏斗从电场区域中央处开始下落．经分选后的颗粒分别装入A．B桶中．混合颗粒离开漏斗进入电场时磷酸盐颗粒带正电，石英颗粒带负电，所有颗粒所带的电量与质量之比均为10–5C/kg．若已知两板间的距离为10cm，颗粒在电场中下落的竖直高度为50cm．设颗粒进入电场时的初速度为零，颗粒间的相互作用力不计．如果要求两种颗粒离开两极板间的电场区域时不接触到极板而且有最大的偏转量．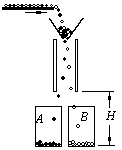
(1)两极板间所加的电压．
(2)若带电平行板的下端距A．B桶底的高度为H=1.0m，求颗粒落至桶底时的速度大小
如图所示，A和B是两个同性点电荷，电量均为q，A固定在绝缘架上，B在A的正上方，且B放在一块绝缘板上，现在手持绝缘板，使B从静止起以加速度a竖直向下做匀加速运动(a＜g)，B的质量为m．
求：(1)B运动到离A多远的地方恰对绝缘板无压力．
(2)如果这个位置正好将初始时B、A高度分成2∶1，B点在此前的运动过程中，电场力和板的支持力对B所做的总功(已知静电力常量为K)．
如下图所示，粗细均匀的长直玻璃管被轻绳倒挂于倾角为θ的斜面上，管内有一段长为h的水银柱(其密度为ρ)封闭着一段空气柱．求在下列情况下，被封闭气体的压强为多少(式中各物理量单位均为国际单位制单位)？
(1)玻璃管静止不动；
(2)剪断细绳后，玻璃管沿斜面保持平稳加速下降过程(知管与斜面间动摩擦因数为μ，且μ＜tanθ)．
A、B两物体叠放着，在光滑的水平面上一起(无相对运动)做简谐运动，如图所示．A、B的质量分别是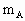
=1kg，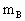
=2kg，相互间最大静摩擦力f=4N，轻质弹簧的劲度系数k=100N／m．试求：
(1)如振幅为0.1m，在振动过程中，静摩擦力的最大值是多少？
(2)为了使A、B不发生相对滑动，振动的振幅最大不超过多少？
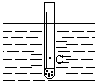
一个截面积为S的均匀直试管内装有适量的砂子，其总重量为G，重心在C点，使它竖直浮在水面上平衡如图所示，若将其用手按下一定的深度，试管将上下振动，试证明试管的运动是简谐运动．
弹簧振子做简谐运动，由a点第一次到达b点用了0.2s，它经过A．b两点时的速度相同．又经过0.4s时间，振子第二次到达b点，在这0.6s时间里振子通过的路程是10cm．求该弹簧振子的周期及振幅．