(本小题满分13分)已知函数 ,.
,.
(Ⅰ) 求函数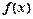 在点(1,
在点(1, )处的切线方程; (Ⅱ) 若函数
)处的切线方程; (Ⅱ) 若函数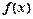 与
与 在区间
在区间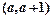 上均为增函数,求
上均为增函数,求 的取值范围; (Ⅲ) 若方程
的取值范围; (Ⅲ) 若方程 有唯一解,试求实数
有唯一解,试求实数 的值.
的值.
.已知等比数列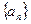 中,且
中,且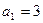 ,
,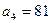 ,求公比
,求公比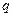 ,通项公式
,通项公式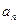 及前
及前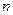 项和
项和 .
.
如图所示,已知ABCD是正方形,PD⊥平面ABCD,PD=AD=2.
(1)求异面直线PC与BD所成的角;
(2)在线段PB上是否存在一点E,使PC⊥平面ADE?若存在,确定E点的位置;若不存在,说明理由.
【必做题】第22题和第23题为必做题, 每小题10分,共20分.要写出必要的文字说明或演算步骤.
有甲、乙两个箱子,甲箱 中有
中有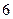 张卡片,其中
张卡片,其中 张写有数字
张写有数字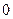 ,
, 张写有数字
张写有数字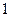 ,
, 张写有数字
张写有数字 ;乙箱中也有
;乙箱中也有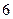 张卡片,其中
张卡片,其中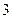 张写有数
张写有数 字
字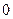 ,
, 张写有数字
张写有数字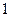 ,
,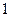 张写有数字
张写有数字 .
.
(1)如果从甲、乙箱中各取一张卡片,设取出的 张卡片上数字之积为
张卡片上数字之积为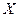 ,求
,求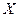 的
的
分布列及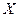 的
的 数学期望;
数学期望;
(2)如果从甲箱中取一张卡片,从乙箱中取两张卡片,那么取出的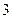 张卡片都写有
张卡片都写有
数字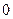 的概率是多少?
的概率是多少?

B.选修4—2 矩阵与变换
已知矩阵
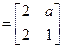 ,其中
,其中 ,若点
,若点 在矩阵
在矩阵 的变换下得到点
的变换下得到点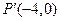 ,
,
(1)求实数a的值;
(2)求矩阵 的特征值及其对应的特征向量.
的特征值及其对应的特征向量.