图(1)是某圆拱形桥一孔圆拱的示意图.这个圆的圆拱跨度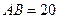 m,拱高
m,拱高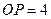 m,建造时每间隔4m需要用一根支柱支撑,求支柱
m,建造时每间隔4m需要用一根支柱支撑,求支柱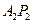 的高度(精确到
的高度(精确到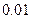 m).
m).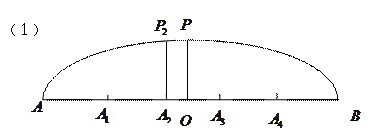
 |
抛物线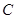 的方程为
的方程为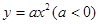 ,过抛物线
,过抛物线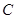 上一点
上一点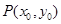 (
( )作斜率为
)作斜率为 的两条直线分别交抛物线
的两条直线分别交抛物线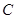 于
于 两点(
两点(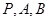 三点互不相同),且满足
三点互不相同),且满足 (
( 且
且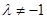 ).
).
(1)求抛物线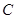 的焦点坐标和准线方程;
的焦点坐标和准线方程;
(2)设直线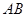 上一点
上一点 ,满足
,满足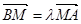 ,证明线段
,证明线段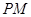 的中点在
的中点在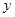 轴上;
轴上;
(3)当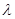 =1时,若点
=1时,若点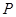 的坐标为
的坐标为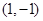 ,求
,求 为钝角时点
为钝角时点 的纵坐标
的纵坐标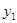 的取值范围.
的取值范围.
已知圆 的方程为:
的方程为: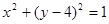 ,直线的方程为
,直线的方程为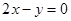 ,点
,点 在直线上,过点
在直线上,过点 作圆
作圆 的切线
的切线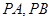 ,切点为
,切点为 .
.
(1)若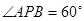 ,求点
,求点 的坐标;
的坐标;
(2)若点 的坐标为
的坐标为 ,过点
,过点 的直线与圆
的直线与圆 交于
交于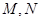 两点,当
两点,当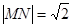 时,求直线
时,求直线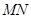 的方程;
的方程;
(3)求证:经过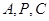 (其中点
(其中点 为圆
为圆 的圆心)三点的圆必经过定点,并求出所有定点的坐标.
的圆心)三点的圆必经过定点,并求出所有定点的坐标.
如图,在底面为平行四边形的四棱锥 中,
中,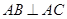 ,
, 平面
平面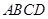 ,且
,且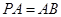 ,点
,点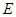 是
是 的中点.
的中点.
(1)求证: ;
;
(2)求二面角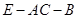 的大小.
的大小.
|

如图, 为圆
为圆 的直径,点
的直径,点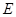 .
.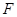 在圆
在圆 上,且
上,且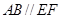 ,矩形
,矩形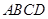 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
,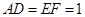 .
.
(1)设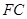 的中点为
的中点为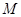 ,求证:
,求证: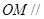 平面
平面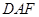 ;
;
(2)求四棱锥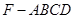 的体积.
的体积.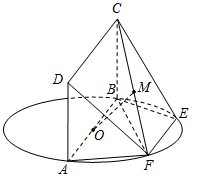
已知命题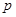 :方程
:方程 所表示的曲线为焦点在
所表示的曲线为焦点在 轴上的椭圆;命题
轴上的椭圆;命题 :实数
:实数 满足不等式
满足不等式 .
.
(1)若命题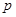 为真,求实数的取值范围;
为真,求实数的取值范围;
(2)若命题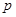 是命题
是命题 的充分不必要条件,求实数
的充分不必要条件,求实数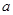 的取值范围.
的取值范围.