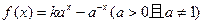
(1)求常数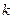 的值;
的值;
(2)若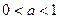 ,
,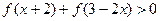 ,求
,求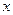 的取值范围;
的取值范围;
(3)若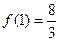 ,且函数
,且函数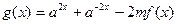 在
在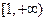 上的最小值为
上的最小值为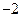 ,求
,求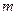 的值
的值
求经过两条直线 :
: 与
与 :
: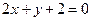 的交点
的交点 ,且垂直于直线
,且垂直于直线 :
: 直线
直线 的方程.
的方程.
棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是B1C1、C1D1的中点,
(1)求证:E、F、B、D四点共面;
(2)求四边形EFDB的面积.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
如图所示,已知空间四边形ABCD,E、F分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且 ,求证直线EF、GH、AC交于一点.
,求证直线EF、GH、AC交于一点.
如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,G为DD1上一点,且D1G:GD=1:2,AC∩BD=O,求证:平面AGO//平面D1EF.
|