已知菱形 的边长为2,对角线
的边长为2,对角线 与
与 交于点
交于点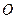 ,且
,且 ,
,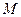 为
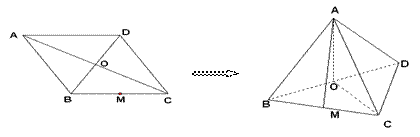
为 的中点.将此菱形沿对角线
的中点.将此菱形沿对角线 折成直二面角
折成直二面角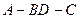 .
.
(I)求证: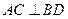 ;
;
(II)求直线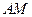 与面
与面 所成角的余弦值大小.
所成角的余弦值大小.
本小题11分
已知圆 的圆心坐标为
的圆心坐标为 ,若圆
,若圆 与
与 轴相切,在直线
轴相切,在直线 上截得的弦长为
上截得的弦长为 ,且圆心在直线
,且圆心在直线 上。
上。
(1)求圆 的方程。
的方程。
(2)若点 圆
圆 上,求
上,求 的取值范围。
的取值范围。
(3)将圆 向左平移一个单位得圆
向左平移一个单位得圆 ,若直线
,若直线 与两坐标轴正半轴的交点分别为
与两坐标轴正半轴的交点分别为 ,直线
,直线 的方程为
的方程为 。当
。当 在坐标轴上滑动且
在坐标轴上滑动且 与圆
与圆 相切时,求
相切时,求 与两坐标轴正半轴围成面积的最小值
与两坐标轴正半轴围成面积的最小值
本小题11分
已知数列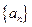 是等差数列,
是等差数列, 11且,
11且, 是数列
是数列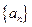 的前
的前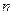 项和。
项和。
(1)求数列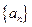 的通项公式
的通项公式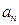 及前
及前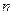 项和
项和 。
。
(2)设正项等比数列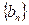 满足
满足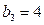 ,
, ,数列
,数列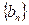 的通项公式
的通项公式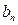
(3)在(2)的条件下若 ,求
,求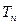 的值。
的值。
本小题9分
如图二某单位建造一间地面面积为12m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x(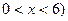 ,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用
,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用
(1)把房屋总造价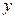 表示成
表示成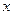 的函数,并写出该函数的定义域。
的函数,并写出该函数的定义域。
|
(2)当侧面的长度为多少时,总造价最底?最低总造价是多少?

本小题8分
如图一线段 所在直线方程为
所在直线方程为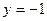 ,线段
,线段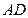 所在直线方程为
所在直线方程为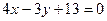 ,线段
,线段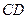 所在直线方程为
所在直线方程为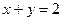 ,求四边形
,求四边形 绕
绕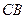 所在直线旋转一周所围成的几何体的表面积和体积
所在直线旋转一周所围成的几何体的表面积和体积
本小题8分
已知直线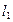 与直线
与直线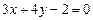 平行且与两坐标轴的正半轴围成的面积为12
平行且与两坐标轴的正半轴围成的面积为12
(1)求直线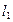 的方程
的方程
(2)若直线 与直线
与直线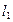 垂直,且与圆
垂直,且与圆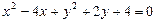 相切,求直线
相切,求直线 的方程。
的方程。