【原创】甲、乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记X为比赛决出胜负时的总局数,求X的分布列和均值(数学期望).
.(本小题满分13分)
如图,椭圆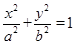 (a>b>0)的上、下顶点分别为A、B,已知点B在直线l:y=-1上,且椭圆的离心率e =
(a>b>0)的上、下顶点分别为A、B,已知点B在直线l:y=-1上,且椭圆的离心率e =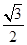 .(Ⅰ)求椭圆的标准方程;
.(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P是椭圆上异于A、B的任意一点,PQ⊥y轴,Q为垂足,M为线段PQ中点,直线AM交直线l于点C,N为线段BC的中点,求证:OM⊥MN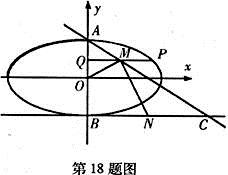
(本小题满分13分)
假设某班级教室共有4扇窗户,在每天上午第三节课上课预备铃声响起时,每扇窗户或被敞开或被关闭,且概率均为0.5,记此时教室里敞开的窗户个数为X .
(Ⅰ)求X的分布列;
(Ⅱ)若此时教室里有两扇或两扇以上的窗户被关闭,班长就会将关闭的窗户全部敞开,否则维持原状不变.记每天上午第三节课上课时该教室里敞开的窗户个数为y,求y的数学期望.
(本小题满分13分)
在数列{a n}中,a1=2,点(a n,a n+1)(n∈N*)在直线y=2x上.
(Ⅰ)求数列{ a n }的通项公式;
(Ⅱ)若bn=log2 an,求数列 的前n项和Tn.
的前n项和Tn.
(本小题满分15分)设函数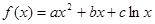 ,(其中
,(其中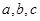 为实常数且
为实常数且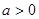 ),曲线
),曲线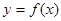 在点
在点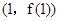 处的切线方程为
处的切线方程为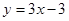 .
.
(Ⅰ) 若函数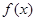 无极值点且
无极值点且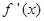 存在零点,求
存在零点,求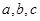 的值;
的值;
(Ⅱ) 若函数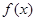 有两个极值点,证明
有两个极值点,证明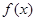 的极小值小于
的极小值小于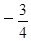 .
.
(本小题满分15分)已知椭圆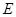 :
: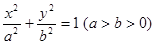 ,设该椭圆上的点到左焦点
,设该椭圆上的点到左焦点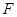
 的最大距离为
的最大距离为 ,到右顶点
,到右顶点
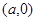 的最大距离为
的最大距离为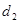 .
.
(Ⅰ) 若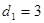 ,
,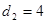 ,求椭圆
,求椭圆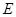 的方程;
的方程;
(Ⅱ) 设该椭圆上的点到上顶点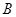
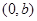 的最大距离为
的最大距离为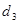 ,求证:
,求证: .
.