己知A,B,C三点坐标分别为(-1,0),(3,-1),(1,2),并且 .
.
(1)求点E,F的坐标
(2)求证: 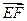 ∥
∥
((本小题满分10分)
选修4—5:不等式选讲 设函数
设函数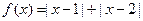
(1)求不等式 的解集;
的解集;
(2)若不等式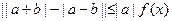 (
( ,
,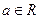 ,
, )恒成立,求实数
)恒成立,求实数 的范围.
的范围.
((本小题满分10分)
选修4—4:坐标系与参数方程
已知直线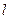 的参数方程为
的参数方程为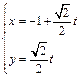 (
(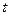 为参数),曲线C的极坐标方程是
为参数),曲线C的极坐标方程是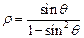 ,以极
,以极 点为原点,极轴为
点为原点,极轴为 轴正方向建立直角坐标系,点
轴正方向建立直角坐标系,点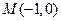 ,直线
,直线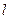 与曲线C交于A、B两点.
与曲线C交于A、B两点.
(1)写出直线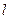 的极坐标方程与曲线C的普通方程;
的极坐标方程与曲线C的普通方程;
(2) 线段MA,MB长度分别记为|MA|,|MB|,求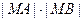 的值.
的值.
(.选修4—1:几何证明选讲
如图,PA切圆O 于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转
于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转 到O D.
到O D.
(1)求线段PD的长;
(2)在如图所示的图形中是否有长度为 的线段?若有,指出该线段;若没有,说明理由.
的线段?若有,指出该线段;若没有,说明理由.
(.(本题满分12分)
已知二次函数 和“伪二次函数”
和“伪二次函数”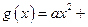
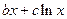 (
(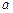 、
、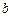 、
、
 ),
),
(I)证明:只要 ,无论
,无论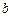 取何值,函数
取何值,函数 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(II)在二次函数 图象上任意取不同两点
图象上任意取不同两点 ,线段
,线段 中点的横坐标为
中点的横坐标为 ,记直线
,记直线 的斜率为
的斜率为 ,
,
( i)求证:
i)求证: ;
;
(ii)对于“伪二次函数” ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论.