(本小题满分15分)已知抛物线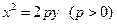 上的一点(m,1)到焦点的距离为
上的一点(m,1)到焦点的距离为 .点
.点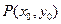 是抛物线上任意一点(除去顶点),过点
是抛物线上任意一点(除去顶点),过点 与
与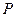 的直线和抛物线交于点
的直线和抛物线交于点 ,过点
,过点 与的
与的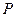 直线和抛物线交于点
直线和抛物线交于点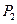 .分别以点
.分别以点 ,
,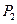 为切点的抛物线的切线交于点P′.
为切点的抛物线的切线交于点P′.
(I)求抛物线的方程;
(II)求证:点P′在y轴上.
 直三棱柱
直三棱柱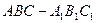 中,
中,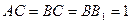 ,
,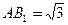 .
.
(1)求证:平面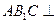 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
已知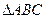 中,
中,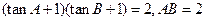 ,求:
,求:
(1)角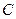 的度数;
的度数;
(2)求三角形 面积的最大值
面积的最大值
已知数列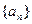 的通项公式是
的通项公式是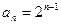 ,数列
,数列 是等差数列,令集合
是等差数列,令集合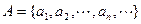 ,
,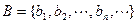 ,
,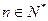 .将集合
.将集合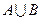 中的元素按从小到大的顺序排列构成的数列记为
中的元素按从小到大的顺序排列构成的数列记为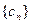 .
.
(1)若 ,
,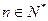 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若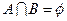 ,数列
,数列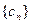 的前5项成等比数列,且
的前5项成等比数列,且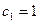 ,
,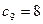 ,求满足
,求满足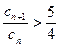
的正整数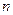 的个数.
的个数.
数列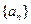 满足:
满足: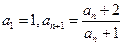
(I)求证: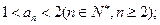
(Ⅱ)令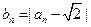
(1)求证: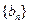 是递减数列;(2)设
是递减数列;(2)设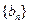 的前
的前 项和为
项和为 求证:
求证:
在一次考试中共有8道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.评分标准规定:“每题只选一个选项,选对得5分,不选或选错得0分”.某考生已确定有4道题答案是正确的,其余题中:有两道只能分别判断2个选项是错误的,有一道仅能判断1个选项是错误的,还有一道因不理解题意只好乱猜,求:
(1)该考生得40分的概率;
(2)该考生得多少分的可能性最大?