已知M、N两点的坐标分别是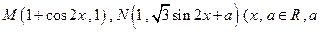 是常数
是常数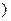 ,令
,令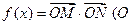 是坐标原点
是坐标原点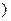 .
.
(Ⅰ)求函数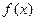 的解析式,并求函数
的解析式,并求函数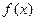 在
在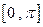 上的单调递增区间;
上的单调递增区间;
(Ⅱ)当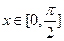 时,
时,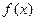 的最大值为
的最大值为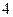 ,求a的值,并说明此时
,求a的值,并说明此时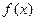 的图象可由函数
的图象可由函数 的图象经过怎样的平移和伸缩变换而得到?
的图象经过怎样的平移和伸缩变换而得到?
关于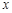 的不等式
的不等式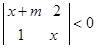 的解集为
的解集为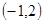 。
。
(1)求实数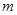 的值;
的值;
(2)若实系数一元二次方程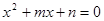 的一个根
的一个根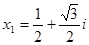 ,求
,求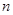 .
.
设等比数列 都在函数
都在函数 的图象上。
的图象上。
(1)求r的值;
(2)当 ;
;
(3)若对一切的正整数n,总有 的取值范围。
的取值范围。
设 ,函数
,函数 ,其中
,其中 是自然对数的底数。
是自然对数的底数。
(1)判断 在R上的单调性;
在R上的单调性;
(2)当 时,求
时,求 在
在 上的最值。
上的最值。
直线 与圆
与圆 交于
交于 、
、 两点,记△
两点,记△ 的面积为
的面积为 (其中
(其中 为坐标原点).
为坐标原点).
(1)当 ,
, 时,求
时,求 的最大值;
的最大值;
(2)当 ,
, 时,求实数
时,求实数 的值.
的值.
在正方体ABCD—A1B1C1D1中,E、F分别为棱BB1和DD1的中点. 
(1)求证:平面B1FC//平面ADE;
(2)试在棱DC上取一点M,使 平面ADE;
平面ADE;
(3)设正方体的棱长为1,求四面体A1—FEA的体积.