在正方体ABCD—A1B1C1D1中，E、F分别为棱BB1和DD1的中点. 
（1）求证：平面B1FC//平面ADE；
（2）试在棱DC上取一点M，使
平面ADE；
（3）设正方体的棱长为1，求四面体A1—FEA的体积.
（本小题满分1６分）已知函数
，其中ｅ是自然数的底数，
。
（1）当
时，解不等式
；
（2）若
在［－１，１］上是单调增函数，求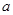
的取值范围；
（3）当
时，求整数ｋ的所有值，使方程
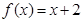在［ｋ，ｋ＋１］上有解。
（本小题满分1６分）平面直角坐标系xoy中，直线
截以原点O为圆心的圆所得的弦长为
（1）求圆O的方程；
（2）若直线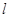
与圆O切于第一象限，且与坐标轴交于D，E，当DE长最小时，求直线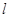的方程；
（3）设M，P是圆O上任意两点，点M关于ｘ轴的对称点为N，若直线MP、NP分别交于ｘ轴于点（ｍ，０）和（ｎ，０），问ｍｎ是否为定值？若是，请求出该定值；若不是，请说明理由。
（本小题满分14分）现有一张长为80cm，宽为60cm的长方形铁皮ABCD，准备用它做成一只无盖长方体铁皮盒，要求材料利用率为100%，不考虑焊接处损失。如图，若长方形ABCD的一个角剪下一块铁皮，作为铁皮盒的底面，用余下材料剪拼后作为铁皮盒的侧面，设长方体的底面边长为x (cm),高为y (cm),体积为V （cm3）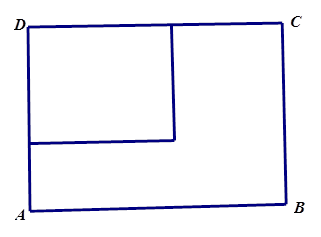
（1）求出x 与 y 的关系式；
（2）求该铁皮盒体积V的最大值；
（本小题满分14分）如图，在直三棱柱
中，AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点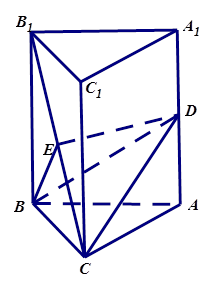
（1）求证：DE∥平面ABC；
（2）求三棱锥E-BCD的体积。
（本小题满分14分）已知向量
，求：
（1）
（2）
的值。