(本小题满分14分)现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失。如图,若长方形ABCD的一个角剪下一块铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3)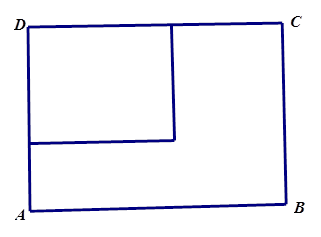
(1)求出x 与 y 的关系式;
(2)求该铁皮盒体积V的最大值;
如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.

(1)试建立适当的坐标系,并写出点P、B、D的坐标;
(2)问当实数a在什么范围时,BC边上能存在点Q,使得PQ⊥QD?
(3)当BC边上有且仅有一个点Q使得PQ⊥QD时,求二面角Q-PD-A的大小.
如图,在四棱锥 中,侧棱
中,侧棱 底面
底面 ,底面
,底面 为矩形,
为矩形, ,
, 为
为 的上一点,且
的上一点,且 ,
, 为PC的中点.
为PC的中点.

(Ⅰ)求证: 平面AEC;
平面AEC;
(Ⅱ)求二面角 的余弦值.
的余弦值.
已知双曲线 ,点
,点 、
、 分别为双曲线
分别为双曲线 的左、右焦点,动点
的左、右焦点,动点 在
在 轴上方.
轴上方.
(1)若点 的坐标为
的坐标为 是双曲线的一条渐近线上的点,求以
是双曲线的一条渐近线上的点,求以 、
、 为焦点且经过点
为焦点且经过点 的椭圆的方程;
的椭圆的方程;
(2)若∠ ,求△
,求△ 的外接圆的方程;
的外接圆的方程;
(3)若在给定直线 上任取一点
上任取一点 ,从点
,从点 向(2)中圆引一条切线,切点为
向(2)中圆引一条切线,切点为 . 问是否存在一个定点
. 问是否存在一个定点 ,恒有
,恒有 ?请说明理由.
?请说明理由.
设函数
(1)当 时,求
时,求 的最大值;
的最大值;
(2)令
 ,以其图象上任意一点
,以其图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 时,方程
时,方程 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.
如图1,在直角梯形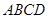 中,
中, ,
,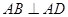 ,且
,且 .
.
现以 为一边向形外作正方形
为一边向形外作正方形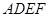 ,然后沿边
,然后沿边 将正方形
将正方形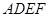 翻折,使平面
翻折,使平面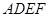 与平面
与平面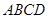 垂直,
垂直,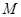 为
为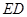 的中点,如图2.
的中点,如图2.
(1)求证: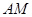 ∥平面
∥平面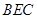 ;
;
(2)求证: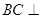 平面
平面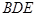 ;
;
(3)求点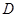 到平面
到平面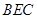 的距离.
的距离.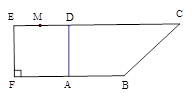

图 图
图