已知双曲线 ,点
,点 、
、 分别为双曲线
分别为双曲线 的左、右焦点,动点
的左、右焦点,动点 在
在 轴上方.
轴上方.
(1)若点 的坐标为
的坐标为 是双曲线的一条渐近线上的点,求以
是双曲线的一条渐近线上的点,求以 、
、 为焦点且经过点
为焦点且经过点 的椭圆的方程;
的椭圆的方程;
(2)若∠ ,求△
,求△ 的外接圆的方程;
的外接圆的方程;
(3)若在给定直线 上任取一点
上任取一点 ,从点
,从点 向(2)中圆引一条切线,切点为
向(2)中圆引一条切线,切点为 . 问是否存在一个定点
. 问是否存在一个定点 ,恒有
,恒有 ?请说明理由.
?请说明理由.
由四个不同的数字1,2,4,x组成无重复数字的三位数.
(1)若x=5,其中能被5整除的共有多少个?
(2)若x=9,其中能被3整除的共有多少个?
(3)若x=0,其中的偶数共有多少个?
(4)若所有这些三位数的各位数字之和是252,求x.
某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
5 |
7 |
9 |
8 |
| 乙班 |
4 |
8 |
9 |
7 |
7 |
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作 和
和 ,试求
,试求 和
和 的分布列和数学期望.
的分布列和数学期望.
(本小题满分10分)已知函数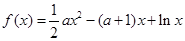 .
.
(1)当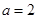 时,求曲线
时,求曲线 在点(1,f(1))处切线的斜率;
在点(1,f(1))处切线的斜率;
(2)当a=3时,求函数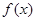 的单调区间.
的单调区间.
(本小题满分13分)已知函数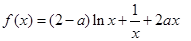 .
.
(Ⅰ)当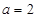 时,求函数
时,求函数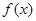 的极值;
的极值;
(Ⅱ)
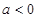 时,讨论
时,讨论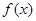 的单调性;
的单调性;
(Ⅲ)若对任意的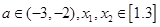 恒有
恒有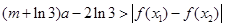 成立,求实数
成立,求实数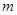 的取值范围.
的取值范围.
(本小题满分13分)已知函数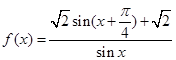 .
.
(Ⅰ)求函数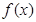 的定义域;
的定义域;
(Ⅱ)若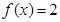 ,求
,求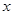 的取值集合及
的取值集合及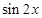 的值.
的值.