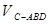(14分)设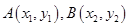 是椭圆
是椭圆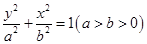 的两点,
的两点,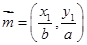 ,
,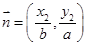 ,且
,且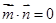 ,椭圆离心率
,椭圆离心率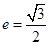 ,短轴长为2,O为坐标原点。
,短轴长为2,O为坐标原点。
(1) 求椭圆方程;
(2) 若存在斜率为 的直线AB过椭圆的焦点
的直线AB过椭圆的焦点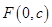 (
(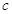 为半焦距),求
为半焦距),求 的值;
的值;
(3) 试问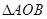 的面积是否为定值?若是,求出该定值;若不是,
的面积是否为定值?若是,求出该定值;若不是, 说明理由。
说明理由。
某高速公路收费站入口处的安全标识墩如图甲所示,墩的上半部分是正四棱锥 ,下半部分是长方体
,下半部分是长方体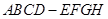 .图乙、图丙分别是该标识墩的正视图和俯视图.
.图乙、图丙分别是该标识墩的正视图和俯视图.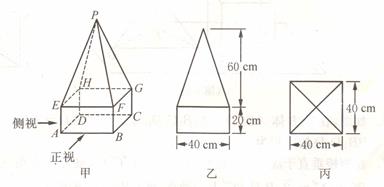
(1)画出该安全标识墩的侧视图,并标出相应的刻度;
(2)求该安全标识墩的体积.
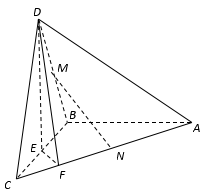
如图,在三棱锥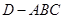 中,已知
中,已知 是正三角形,
是正三角形,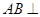 平面
平面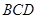 ,
,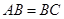 ,
,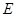 为
为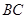 的中点,
的中点,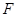 在棱
在棱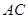 上,且
上,且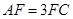 ,
, 
(1)求证: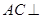 平面
平面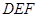 ;
;
(2)若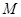 为
为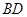 的中点,问
的中点,问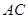 上是否存在一点
上是否存在一点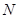 ,使
,使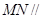 平面
平面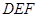 ?若存在,说明点
?若存在,说明点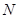 的位置;若不存在,试说明理由;
的位置;若不存在,试说明理由;
如图,四棱锥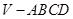 的底面
的底面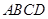 是边长为2的正方形,其他四个侧面都是侧棱长为
是边长为2的正方形,其他四个侧面都是侧棱长为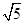 的等腰三角形.若
的等腰三角形.若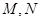 分别为棱
分别为棱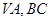 的中点,
的中点,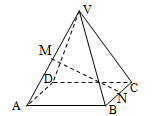
(1)求证: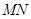 ∥侧面
∥侧面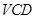 ;
;
(2)试求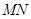 与底面
与底面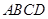 所成角的正弦值.
所成角的正弦值.
在平面直角坐标系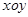 中,曲线
中,曲线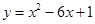 与坐标轴的交点都在圆
与坐标轴的交点都在圆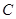 上
上
(1)求圆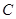 的方程;
的方程;
(2)若圆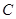 与直线
与直线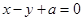 交于
交于 两点,且
两点,且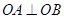 ,求
,求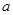 的值.
的值.
如图,在四面体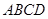 中,
中,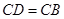 ,
,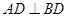 ,点
,点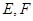 分别是
分别是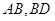 的中点
的中点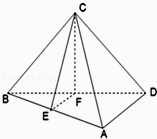
(1)求证:平面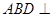 平面
平面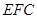 ;
;
(2)当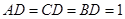 ,且
,且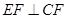 时,求三棱锥
时,求三棱锥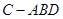 的体积
的体积