某高速公路收费站入口处的安全标识墩如图甲所示,墩的上半部分是正四棱锥 ,下半部分是长方体
,下半部分是长方体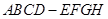 .图乙、图丙分别是该标识墩的正视图和俯视图.
.图乙、图丙分别是该标识墩的正视图和俯视图.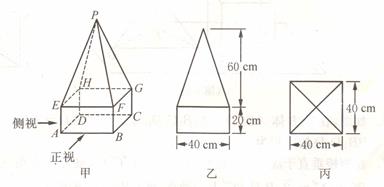
(1)画出该安全标识墩的侧视图,并标出相应的刻度;
(2)求该安全标识墩的体积.
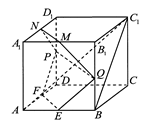
如图,在正方体
中,
,
,
,
,
,
分别是棱
,
,
,
,
,
的中点.求证:
(1)直线
∥平面
;
(2)直线
⊥平面
.
某实验室一天的温度(单位:
)随时间
(单位:
)的变化近似满足函数关系;
.
(1)求实验室这一天上午8时的温度;
(2)求实验室这一天的最大温差.
已知函数
.
(1)求
在区间
上的最大值;
(2)若过点
存在3条直线与曲线
相切,求
的取值范围;
(3)问过点
分别存在几条直线与曲线
相切?(只需写出结论)
已知椭圆 .
(1)求椭圆C的离心率;
(2)设
为原点,若点
在直线
,点
在椭圆
上,且
,求线段
长度的最小值.
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图: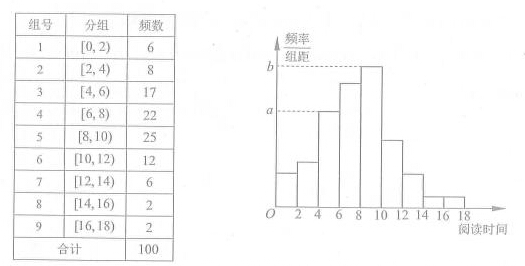
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的
的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)