如图1,⊙O的直径AB=4,点C、D为⊙O上两点,且∠CAB=45o,F为 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).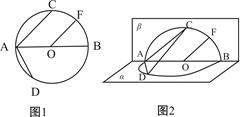
(Ⅰ)求证:OF//平面ACD;
(Ⅱ)在 上是否存在点
上是否存在点 ,使得平面
,使得平面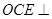 平面ACD?若存在,试指出点
平面ACD?若存在,试指出点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(本小题满分14分)已知函数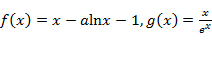 ,其中a为实数.
,其中a为实数.
(1)求g(x)的极值;
(2)设a<0,若对任意的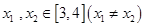 ,
, 恒成立,求a的最小值.
恒成立,求a的最小值.
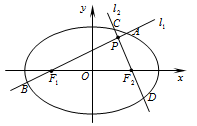
(本小题满分13分)如图,分别过椭圆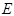 :
: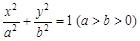 左右焦点
左右焦点 、
、 的动直线
的动直线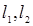 相交于
相交于 点,与椭圆
点,与椭圆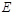 分别交于
分别交于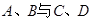 不同四点, 直线
不同四点, 直线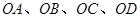 的斜率
的斜率 、
、 、
、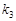 、
、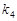 满足
满足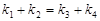 .已知当
.已知当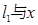 轴重合时,
轴重合时,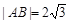 ,
,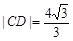 .
.
(1)求椭圆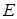 的方程;
的方程;
(2)是否存在定点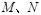 ,使得
,使得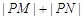 为定值.若存在,求出
为定值.若存在,求出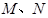 点坐标并求出此定值,若不存在,说明理由.
点坐标并求出此定值,若不存在,说明理由.
(本小题满分13分)某工厂生产A,B两种型号的玩具,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种玩具各100件进行检测,检测结果统计如下:
| 测试指标 |
[70,76) |
[76,82) |
[82,88) |
[88,94) |
[94,100) |
| 玩具A |
8 |
12 |
40 |
32 |
8 |
| 玩具B |
7 |
18 |
40 |
29 |
6 |
(Ⅰ)试分别估计玩具A、玩具B为正品的概率;
(Ⅱ)生产一件玩具A,若是正品可盈利40元,若是次品则亏损5元;生产一件玩具B,若是正品可盈利50元,若是次品则亏损10元.在(I)的前提下,
(i)记X为生产1件玩具A和1件玩具B所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件玩具B所获得的利润不少于140元的概率.
(本小题满分13分)如图,在三棱柱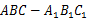 ,
, ⊥平面ABC,BC⊥AC,BC=AC=2,D为AC的中点.
⊥平面ABC,BC⊥AC,BC=AC=2,D为AC的中点.
(1)求证: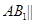 平面
平面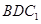 ;
;
(2)若二面角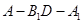 大小为
大小为 ,求直线
,求直线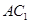 与
与 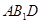 所成角的大小.
所成角的大小.
(本小题满分13分)已知函数 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若在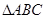 中,角
中,角 ,
,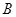 ,
, 的对边分别为
的对边分别为 ,
, ,
,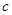 ,
, ,
, 为锐角,且
为锐角,且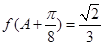 ,求
,求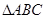 面积
面积 的最大值.
的最大值.