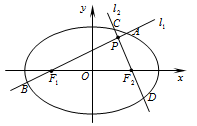
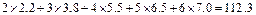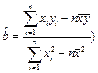(本小题满分13分)如图,分别过椭圆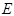 :
: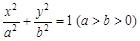 左右焦点
左右焦点 、
、 的动直线
的动直线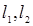 相交于
相交于 点,与椭圆
点,与椭圆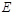 分别交于
分别交于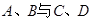 不同四点, 直线
不同四点, 直线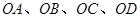 的斜率
的斜率 、
、 、
、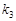 、
、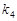 满足
满足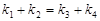 .已知当
.已知当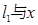 轴重合时,
轴重合时,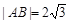 ,
,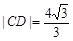 .
.
(1)求椭圆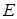 的方程;
的方程;
(2)是否存在定点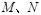 ,使得
,使得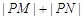 为定值.若存在,求出
为定值.若存在,求出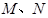 点坐标并求出此定值,若不存在,说明理由.
点坐标并求出此定值,若不存在,说明理由.
已知各项都不相等的等差数列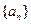 的前6项和为60,且
的前6项和为60,且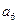 为
为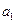 和
和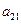 的等比中项.
的等比中项.
( I )求数列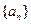 的通项公式;
的通项公式;
(II) 若数列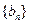 满足
满足 ,且
,且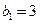 ,求数列
,求数列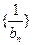 的前
的前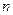 项和
项和 .
.
在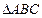 中,
中,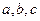 分别是角
分别是角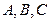 的对边,向量
的对边,向量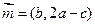 ,
,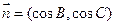 ,且
,且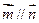 .
.
(Ⅰ)求角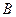 的大小;
的大小;
(Ⅱ)设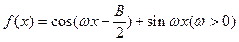 ,且
,且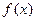 的最小正周期为
的最小正周期为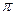 ,求
,求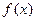 在区间
在区间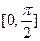 上的最大值和最小值.
上的最大值和最小值.
设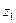 ,
, 为共轭复数,且
为共轭复数,且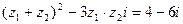 ,求
,求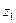 和
和 。
。
已知:如图,⊙O与⊙P相 交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长
交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长 线交⊙P于D,E两点,过点E作EF⊥CE交CB延长线于点F.若CD=2,CB=2
线交⊙P于D,E两点,过点E作EF⊥CE交CB延长线于点F.若CD=2,CB=2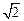 ,求E
,求E F的长.
F的长.
下表是关于某设备的使用年限(年)和所需要的维修费用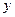 (万元)的几组统计数据:
(万元)的几组统计数据:
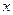 |
2 |
3 |
4 |
5 |
6 |
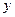 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(1)请在给出的坐标系中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出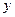 关于
关于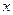 的线性回归方程
的线性回归方程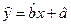 ;
;
(3)估计使用年限为10年时,维修费用为多少?
(参考数值或公式