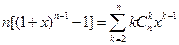(本小题满分13分)某工厂生产A,B两种型号的玩具,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种玩具各100件进行检测,检测结果统计如下:
| 测试指标 |
[70,76) |
[76,82) |
[82,88) |
[88,94) |
[94,100) |
| 玩具A |
8 |
12 |
40 |
32 |
8 |
| 玩具B |
7 |
18 |
40 |
29 |
6 |
(Ⅰ)试分别估计玩具A、玩具B为正品的概率;
(Ⅱ)生产一件玩具A,若是正品可盈利40元,若是次品则亏损5元;生产一件玩具B,若是正品可盈利50元,若是次品则亏损10元.在(I)的前提下,
(i)记X为生产1件玩具A和1件玩具B所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件玩具B所获得的利润不少于140元的概率.
某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰。已知某选手能正确回答第一、二、三、四轮的问题的概率分别为 且各轮问题能否正确回答互不影响。
且各轮问题能否正确回答互不影响。
(Ⅰ)求该选手进入第四轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率
已知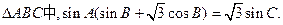
(Ⅰ)求角A的大小 ;
;
(Ⅱ)若BC=3,求 周长的取值范围。
周长的取值范围。
设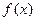 是定义在[-1,1]上的奇函数,且对任意
是定义在[-1,1]上的奇函数,且对任意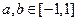 ,当
,当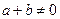 时,都有
时,都有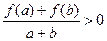 .
.
(1)若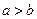 ,试比较
,试比较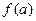 与
与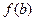 的大小;
的大小;
(2)解不等式
(3)如果 和
和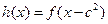 这两个函数的定义域的交集为空集,求
这两个函数的定义域的交集为空集,求 的取值范围.
的取值范围.
在数列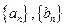 中,
中, 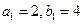 ,且
,且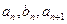 成等差数列,
成等差数列, 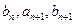 成等比数列
成等比数列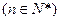 .
.
(1)求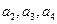 及
及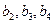 ,由此猜测
,由此猜测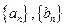 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(2)证明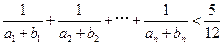 .
.
请先阅读:在等式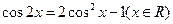 的两边对x求导
的两边对x求导
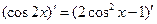 .由求导法则得
.由求导法则得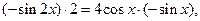 化简后得等式
化简后得等式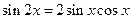 利用上述想法(或者其他方法),试由等式
利用上述想法(或者其他方法),试由等式
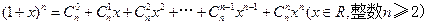 ,
,
证明