已知圆C经过点 ,且圆心在直线
,且圆心在直线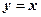 上,且,又直线
上,且,又直线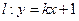 与圆C相交于
与圆C相交于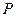 、
、 两点.
两点.
(I)求圆C的方程;
(II)若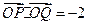 ,求实数
,求实数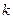 的值;
的值;
(III)过点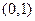 作直线
作直线 与
与 垂直,且直线
垂直,且直线 与圆C交于
与圆C交于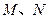 两点,求四边形
两点,求四边形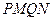 面积的最大值.
面积的最大值.
已知三棱柱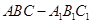 中,平面
中,平面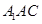 ⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。
⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。
(Ⅰ)求证:AC1⊥平面A1BC;
(Ⅱ)求平面AA1B与平面A1BC的夹角的余弦值。
正项数列 的前n项和为
的前n项和为 ,且
,且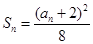 。
。
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)求证: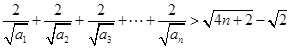 。
。
方便、快捷、实惠的电动车是很多人的出行工具。可是,随着电动车的普及,它的安全性也越来越受到人们关注。为了出行更安全,交通部门限制电动车的行驶速度为24km/h。若某款电动车正常行驶遇到紧急情况时,紧急刹车时行驶的路程S(单位:m)和时间t(单位:s)的关系为: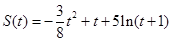 。
。
(Ⅰ)求从开始紧急刹车至电动车完全停止所经过的时间;
(Ⅱ)求该款车正常行驶的速度是否在限行范围内?
已知a,b,c分别为△ABC三个内角A,B,C的对边,且 。
。
(Ⅰ)求B;
(2)若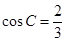 ,求
,求 的值。
的值。
已知函数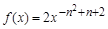
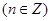 满足
满足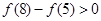 .
.
(1)求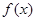 的解析式;
的解析式;
(2)对于(1)中得到的函数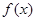 ,试判断是否存在
,试判断是否存在 ,使
,使 在区间
在区间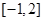 上的值域为
上的值域为 ?若存在,求出
?若存在,求出 ;若不存在,请说明理由.
;若不存在,请说明理由.