已知直线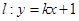 过定点
过定点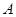 ,动点
,动点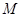 满足
满足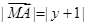 ,动点
,动点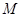 的轨迹为
的轨迹为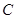 .
.
(Ⅰ)求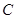 的方程;
的方程;
(Ⅱ)直线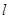 与
与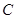 交于
交于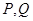 两点,以
两点,以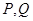 为切点分别作
为切点分别作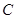 的切线,两切线交于点
的切线,两切线交于点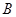 .
.
①求证: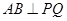 ;②若直线
;②若直线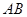 与
与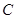 交于
交于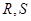 两点,求四边形
两点,求四边形 面积的最大值.
面积的最大值.
如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C, 的平分线分别交AB、AC于点D、E.
的平分线分别交AB、AC于点D、E.
(Ⅰ)证明:
(Ⅱ)若AC=AP,求 的值
的值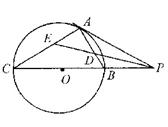
已知函数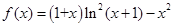 ,
,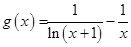 .
.
(Ⅰ)判定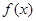 在
在 上的单调性;
上的单调性;
(Ⅱ)求 在
在 上的最小值;
上的最小值;
(Ⅲ)若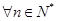 ,
, 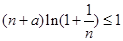 ,求实数
,求实数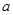 的取值范围.
的取值范围.
如图,曲线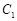 是以原点O为中心、
是以原点O为中心、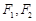 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以O为顶点、
是以O为顶点、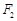 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线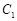 和
和 的交点且
的交点且 为钝角,若
为钝角,若 ,
,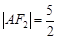 .
.
(Ⅰ)求曲线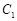 和
和 的方程;
的方程;
(Ⅱ)过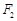 作一条与
作一条与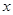 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线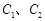 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问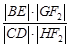 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
已知四边形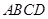 满足
满足 ∥
∥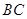 ,
,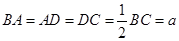 ,
,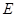 是
是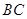 的中点,将
的中点,将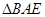 沿着
沿着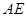 翻折成
翻折成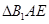 ,使面
,使面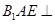 面
面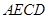 ,
,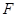 为
为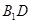 的中点.
的中点. 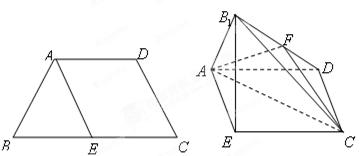
(Ⅰ)求四棱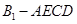 的体积;
的体积;
(Ⅱ)证明: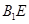 ∥面
∥面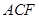 ;
;
(Ⅲ)求面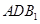 与面
与面 所成二面角的余弦值.
所成二面角的余弦值.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如右图).记成绩不低于90分者为“成绩优秀”.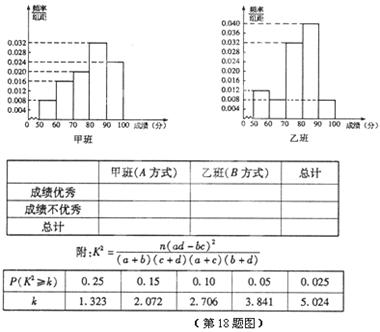
(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为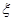 ,求
,求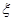 的分布列和数学期望;
的分布列和数学期望;
(II)根据频率分布直方图填写下面 列联表,并判断是否有95%的把握认为“成绩优秀”与教学方式有关。
列联表,并判断是否有95%的把握认为“成绩优秀”与教学方式有关。