已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量
为取出3球所得分数之和.
(Ⅰ)求
的分布列;
(Ⅱ)求
的数学期望
.
已知函数
(1)当
时,求不等式
的解集;
(2)若
的解集包含
,求
的取值范围.
已知曲线 的参数方程是 ,以坐标原点为极点, 轴的正半轴为极轴建立坐标系,曲线 的坐标系方程是 ,正方形 的顶点都在 上,且 依逆时针次序排列,点 的极坐标为
(1)求点
的直角坐标;
(2)设
为
上任意一点,求
的取值范围.
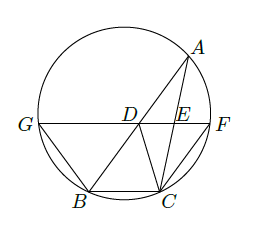
如图,
分别为
边
的中点,直线
交
的外接圆于
两点,若
,证明:
(1)
;
(2)
已知函数
满足满足
;
(1)求
的解析式及单调区间;
(2)若
,求
的最大值.