已知函数f(x)=|x﹣4|﹣t,t∈R,且关于x的不等式f(x+2)≤2的解集为[﹣1,5].
(1)求t值;
(2)a,b,c均为正实数,且a+b+c=t,求证: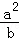 +
+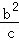 +
+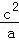 ≥1.
≥1.
在直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的圆心的极坐标为( ,
,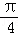 ),半径r=
),半径r= ,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
(1)求圆C的直角坐标方程;
(2)求|PA|•|PB|的值.
如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,连接AC,过点A作AD⊥CD于点D,交⊙O于点E.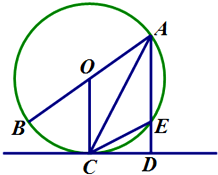
(Ⅰ)证明:∠AOC=2∠ACD;
(Ⅱ)证明:AB•CD=AC•CE.
已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,(a为常数,e为自然对数的底,e≈2.71828).
(1)当a=1时,求f(x)的单调区间;
(2)若f(x)>0在区间(0, )上恒成立,求a的最小值.
)上恒成立,求a的最小值.
如图,已知椭圆 的右顶点为A(2,0),点P(2e,
的右顶点为A(2,0),点P(2e, )在椭圆上(e为椭圆的离心率).
)在椭圆上(e为椭圆的离心率).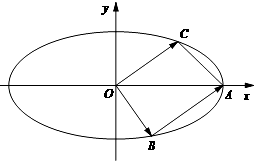
(1)求椭圆的方程;
(2)若点B,C(C在第一象限)都在椭圆上,满足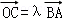 ,且
,且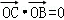 ,求实数λ的值.
,求实数λ的值.