盒子装中有形状、大小完全相同的五张卡片,分别标有数字1,2,3,4,5.现每次从中任意抽取一张,取出后不再放回.
(1)若抽取三次,求前两张卡片所标数字之和为偶数的条件下,第三张为奇数的概率;
(2)若不断抽取,直至取出标有偶数的卡片为止,设抽取次数为ξ,求随机变量ξ的分布列及数学期望.
对甲、乙两种商品的重量的误差进行抽查,测得数据如下(单位: ):
):
甲:13 15 14 14 9 14 21 9 10 11
乙:10 14 9 12 15 14 11 19 22 16
(1)画出样本数据的茎叶图,并指出甲,乙两种商品重量误差的中位数;
(2)计算甲种商品重量误差的样本方差;
(3)现从重量误差不低于15的乙种商品中随机抽取两件,求重量误差为19的商品被抽
中的概率。
已知向量
 函数
函数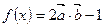
(1)求函数 的解析式,并写出函数
的解析式,并写出函数 图象的对称中心坐标与对称轴方程.
图象的对称中心坐标与对称轴方程.
(2)求函数 的单调递增区间;
的单调递增区间;
(本小题满分12分)
已知函数 ,
,
(1)求 的单调区间;
的单调区间;
(2) 若对任意的
若对任意的 ,都存在
,都存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。
(本小题满分12分)
已知 是椭圆
是椭圆 :
: 的右焦点,也是抛物线
的右焦点,也是抛物线 的焦点,点P为
的焦点,点P为 与
与 在第一象限的交点,且
在第一象限的交点,且 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若椭圆 的左、右顶点分别为
的左、右顶点分别为 ,过
,过 的直线交
的直线交 于
于 两点,记
两点,记 的面积分别为
的面积分别为 ,求
,求 的取值范围。
的取值范围。
(本小题满分12分)
已知数列 中,
中, ,
, ,其前
,其前 项和
项和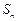 满足
满足 ;数列
;数列 中,
中, ,
,
 .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设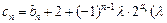 为非零整数,
为非零整数,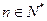 ),试确定
),试确定 的值,使得对任意
的值,使得对任意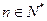 ,都有
,都有 成立.
成立.