(本小题满分12分)
已知数列 中,
中, ,
, ,其前
,其前 项和
项和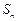 满足
满足 ;数列
;数列 中,
中, ,
,
 .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设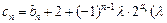 为非零整数,
为非零整数,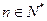 ),试确定
),试确定 的值,使得对任意
的值,使得对任意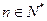 ,都有
,都有 成立.
成立.
某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售 、
、 两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的大数据统计分析,
两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的大数据统计分析, 品牌的销售利润
品牌的销售利润 与投入资金
与投入资金 成正比,其关系如图1所示,
成正比,其关系如图1所示, 品牌的销售利润
品牌的销售利润 与投入资金
与投入资金 的算术平方根成正比,其关系如图2所示(利润与资金的单位:万元).
的算术平方根成正比,其关系如图2所示(利润与资金的单位:万元).
(1)分别将 、
、 两个品牌的销售利润
两个品牌的销售利润 、
、 表示为投入资金
表示为投入资金 的函数关系式;
的函数关系式;
(2)该商场计划投入5万元经销该种商品,并全部投入 、
、 两个品牌,问:怎样分配这5万元资金,才能使经销该种商品获得最大利润,其最大利润为多少万元?
两个品牌,问:怎样分配这5万元资金,才能使经销该种商品获得最大利润,其最大利润为多少万元?
已知 为复数,
为复数, 为实数,且
为实数,且 为纯虚数,其中i是虚数单位.
为纯虚数,其中i是虚数单位.
(1)求复数 ;
;
(2)若复数 满足
满足 ,求
,求 的最小值.
的最小值.
已知命题 ,
, .
.
(1)若 ,求
,求 的值;
的值;
(2)若 ,求
,求 的取值范围.
的取值范围.
已知函数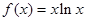 .
.
(1)若直线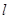 过点
过点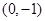 ,并且与曲线
,并且与曲线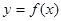 相切,求直线
相切,求直线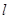 的方程;
的方程;
(2)设函数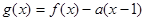 ,其中
,其中 ,求函数
,求函数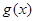 在
在 上的最小值.(其中
上的最小值.(其中 为自然对数的底数)
为自然对数的底数)
已知椭圆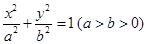 的长轴长为4,且点
的长轴长为4,且点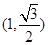 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)过椭圆右焦点斜率为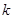 的直线
的直线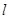 交椭圆于
交椭圆于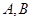 两点,若
两点,若 ,求直线
,求直线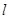 的方程
的方程