某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
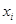 (月) (月) |
 |
 |
 |
 |
 |
 (千克) (千克) |
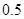 |
 |
 |
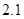 |
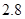 |
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图.

(2)请根据上表提供的数据,用最小二乘法求出变量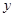 关于变量
关于变量 的线性回归直线方程
的线性回归直线方程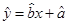 .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: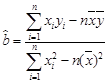 ,
,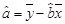 )
)
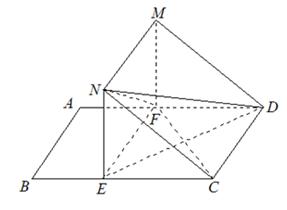
如图,矩形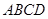 中,
中,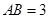 ,
,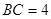 .
.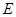 ,
,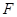 分别在线段
分别在线段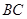 和
和 上,
上,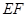 ∥
∥ ,将矩形
,将矩形 沿
沿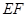 折起.记折起后的矩形为
折起.记折起后的矩形为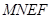 ,且平面
,且平面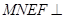 平面
平面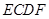 .
.
(Ⅰ)求证: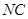 ∥平面
∥平面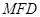 ;
;
(Ⅱ)若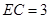 ,求证:
,求证: ;
;
(Ⅲ)求四面体 体积的最大值.
体积的最大值.
现对某市工薪阶层关于“楼市限购政策”的态度进行调查,随机抽查了50人,他们月收入(单位:百元)的频数分布及对“楼市限购政策”赞成人数如下表:
| 月收入(单位百元) |
[15,25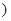 |
[25,35 |
[35,45 |
[45,55 |
[55,65 |
[65,75 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(Ⅰ)根据以上统计数据填写下面2×2列联表,并回答是否有99%的把握认为月收入以5500元为分界点对“楼市限购政策” 的态度有差异?
| 月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
|
| 赞成 |
 |
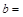 |
|
| 不赞成 |
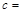 |
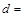 |
|
| 合计 |
(Ⅱ)若从月收入在[55,65)的被调查对象中随机选取两人进行调查,求至少有一人不赞成“楼市限购政策”的概率.
(参考公式: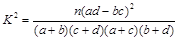 ,其中
,其中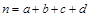 .)
.)
参考值表:
P( ) ) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知函数 .
.
(Ⅰ)求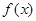 的单调递增区间;
的单调递增区间;
(Ⅱ)在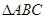 中,角
中,角 ,
,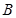 ,
,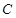 的对边分别为
的对边分别为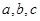 .已知
.已知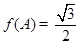 ,
,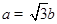 ,试判断
,试判断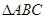 的形状.
的形状.
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为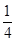 .
.
(Ⅰ)求甲乙二人中至少有一人破译出密码的概率;
(Ⅱ)求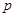 的值;
的值;
(Ⅲ)设甲、乙、丙三人中破译出密码的人数为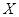 ,求
,求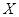 的分布列和数学期望
的分布列和数学期望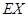 .
.
已知数列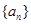 中,
中,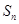 是
是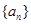 的前
的前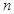 项和,且
项和,且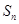 是
是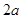 与
与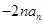 的等差中项,其中
的等差中项,其中 是不等于零的常数.
是不等于零的常数.
(1)求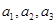 ; (2)猜想
; (2)猜想 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明.