已知抛物线 上一点 到其焦点的距离为 .
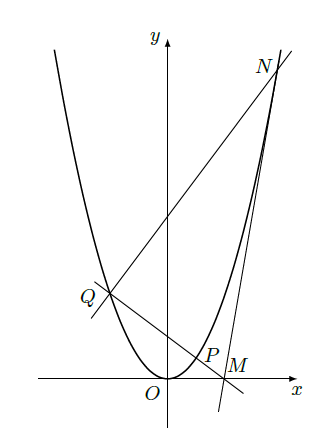
(Ⅰ)求 p于 m的值;
(Ⅱ)设抛物线C上一点 p的横坐标为 t( t>0),过 p的直线交C于另一点 Q,交 x轴于 M点,过点 Q作 PQ的垂线交 C于另一点 N.若 MN是 C的切线,求 t的最小值;
(本小题满分10分)
(1)等差数列{ }中,已知a1=
}中,已知a1= ,a2+a5=4,
,a2+a5=4, =33,试求n的值.
=33,试求n的值.
(2)在等比数列{ }中,a5=162,公比q=3,前n项和
}中,a5=162,公比q=3,前n项和 =242,求首项a1和项数n.
=242,求首项a1和项数n.
在平面直角坐标系 中,已知以O为圆心的圆与直线
中,已知以O为圆心的圆与直线 恒有公共点,且要求使圆O的面积最小.
恒有公共点,且要求使圆O的面积最小.
(1)写出圆O的方程;
(2)圆O与x轴相交于A、B两点,圆内动点P使 、
、 、
、 成等比数列,求
成等比数列,求 的范围;
的范围;
(3)已知定点Q(−4,3), 直线
直线 与圆O交于M、N两点,试判断
与圆O交于M、N两点,试判断 是否有最大值,若存在求出最大值,并求出此时直线
是否有最大值,若存在求出最大值,并求出此时直线 的方程,若不存在,给出理由.
的方程,若不存在,给出理由.
如图,在直四棱柱 中,已知
中,已知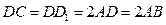 ,
, .
.
(1)求证: ;
;
(2)设 是
是 上一点,试确定
上一点,试确定 的位置,使
的位置,使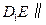 平面
平面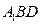 ,并证明.
,并证明.
已知命题p:“∀x∈[1,2],x2-a≥0”,命题q:“∃x∈R, +2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围.
+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围.
如图,平行四边形 中,
中, ,
, 将
将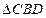 沿
沿 折起到
折起到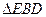 的位置,使平面
的位置,使平面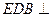 平面
平面
(I)求证: (Ⅱ)求三棱锥
(Ⅱ)求三棱锥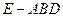 的侧面积。
的侧面积。