(本小题满分12分)
已知 是椭圆
是椭圆 :
: 的右焦点,也是抛物线
的右焦点,也是抛物线 的焦点,点P为
的焦点,点P为 与
与 在第一象限的交点,且
在第一象限的交点,且 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若椭圆 的左、右顶点分别为
的左、右顶点分别为 ,过
,过 的直线交
的直线交 于
于 两点,记
两点,记 的面积分别为
的面积分别为 ,求
,求 的取值范围。
的取值范围。
若四位数 的各位数码
的各位数码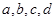 中,任三个数码皆可构成一个三角形的三条边长,则称为四位三角形数,定义
中,任三个数码皆可构成一个三角形的三条边长,则称为四位三角形数,定义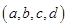 为的数码组,其中
为的数码组,其中 若 数码组为
若 数码组为 型,
型, , 试求所有四位三角形数的个数.
, 试求所有四位三角形数的个数.
已知棱长为1的正方体AC1,E、F分别是B1C1、C1D的中点.
(1)求点A1到平面的BDEF的距离;
(2)求直线A1D与平面BDEF所成的角.
已知在 的展开式中,第6项
的展开式中,第6项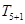 为常数项.
为常数项.
(1)求n;
(2)问展开式中的有理项.分别为第几项?说明理由。
7名师生站成一排照相留念,其中老师1人,男生4人,女生2人,在下列情况下,各有不同站法多少种?(用数字作答)
(1)两名女生必须相邻而站;
(2)4名男生互不相邻.
已知函数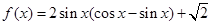 ,
,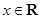 .
.
(1)求函数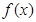 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)求函数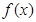 在区间
在区间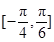 上的最小值和最大值;
上的最小值和最大值;
(3)若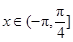 ,求使
,求使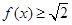 的
的 取值范围.
取值范围.