已知过曲线 上任意一点
上任意一点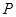 作直线
作直线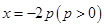 的垂线,垂足为
的垂线,垂足为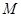 ,且
,且 .
.
⑴求曲线 的方程;
的方程;
⑵设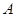 、
、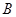 是曲线
是曲线 上两个不同点,直线
上两个不同点,直线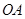 和
和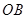 的倾斜角分别为
的倾斜角分别为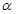 和
和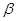 ,当
,当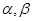 变化且
变化且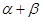 为定值
为定值 时,证明直线
时,证明直线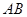 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
已知函数
,曲线
在点
处的切线方程为
。
(1)求
、
的值;
(2)如果当
,且
时,
,求
的取值范围。
在平面直角坐标系 中,已知点 点在直线 上, 点满足 , 点的轨迹为曲线 .
(1)求
的方程;
(2)
为
上的动点,
为
在
点处得切线,求
点到
距离的最小值.
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为 配方和 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
配方的频数分布表

配方的频数分布表

(1)分别估计用
配方,
配方生产的产品的优质品率;
(2)已知用B配方生成的一件产品的利润
(单位:元)与其质量指标值
的关系式为
,
从用
配方生产的产品中任取一件,其利润记为
(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
如图,四棱锥
中,底面
为平行四边形,
,
,
.
(1)证明:
;
(2)若
,求二面角
的余弦值。
等比数列 的各项均为正数,且
(1)求数列
的通项公式;
(2)设
求数列
的前
项和.