如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.

(1)试建立适当的坐标系,并写出点P、B、D的坐标;
(2)问当实数a在什么范围时,BC边上能存在点Q,使得PQ⊥QD?
(3)当BC边上有且仅有一个点Q使得PQ⊥QD时,求二面角Q-PD-A的大小.
在△ABC中,角A,B,C的对边分别为a,b,c.已知
(1)求角A的大小;
(2)若 ,△ABC的面积为
,△ABC的面积为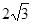 ,求
,求 .
.
如图,四棱锥 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中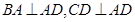 ,
,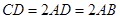 ,平面
,平面 底面
底面 ,
,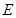 是
是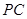 的中点.
的中点.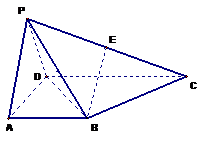
(1)求证: //平面
//平面 ;
;
(2)求证: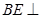
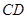 ;
;
(3)求 与平面
与平面 所成角的正弦值。
所成角的正弦值。
已知曲线C上的动点P(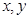 )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
(1)求曲线C的方程。
(2)过点M(1,2)的直线 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线 的方程。
的方程。
已知下列三个方程: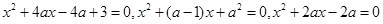 至少有一个方程有实数根.求实数
至少有一个方程有实数根.求实数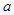 的取值范围.
的取值范围.
设命题p:实数x满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足 .
.
(1)若 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是
 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.