如图,四棱锥 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中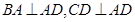 ,
,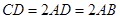 ,平面
,平面 底面
底面 ,
,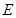 是
是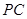 的中点.
的中点.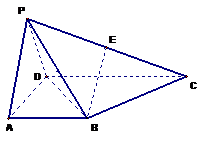
(1)求证: //平面
//平面 ;
;
(2)求证: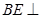
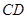 ;
;
(3)求 与平面
与平面 所成角的正弦值。
所成角的正弦值。
已知(x,y)在映射f下的象是(x+y,x2-y),其中x≥0,求:(2,-2)的原象.
已知集合A=R,B={(x,y)|x,y∈R},f:A→B是从A到B的映射,
f:x→(x+1,x2+1),求A中元素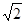 的象和B中元素(
的象和B中元素( )的原象.
)的原象.
求下列函数的定义域:
(1)y=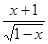
⑵y=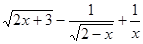
用长为 的铁丝弯成下部为矩形,上部为半圆形的框架,若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并指出其定义域.
的铁丝弯成下部为矩形,上部为半圆形的框架,若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并指出其定义域.
在极坐标系中,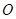 为极点,半径为2的圆
为极点,半径为2的圆 的圆心的极坐标为
的圆心的极坐标为 .
.
(1)求圆 极坐标方程;
极坐标方程;
(2)在以极点为原点,以极轴为 轴正半轴建立的直角坐标系中,直线
轴正半轴建立的直角坐标系中,直线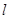 的参数方程
的参数方程
为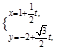 (
( 为参数),直线
为参数),直线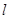 与圆
与圆 相交于
相交于 、
、 两点,已知定点
两点,已知定点 ,
,
求 .
.