(本小题满分16分)平面直角坐标系xoy中,直线 截以原点O为圆心的圆所得的弦长为
截以原点O为圆心的圆所得的弦长为
(1)求圆O的方程;
(2)若直线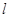 与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线
与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线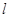 的方程;
的方程;
(3)设M,P是圆O上任意两点,点M关于x轴的对称点为N,若直线MP、NP分别交于x轴于点(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由。
若向量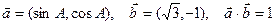 ,且
,且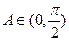
(1)求 ;
;
(2)求函数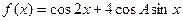 的值域
的值域
.求同时满足下列条件的所有的复数z,
①z+ ∈R, 且1<z+
∈R, 且1<z+ ≤6;
≤6;
②z的实部和虚部都是整数.
.从4名男生和2名女生中任选3人参加演讲比赛,设随机变量 表示所选3人中女生的人数.
表示所选3人中女生的人数.
(1)求 的分布列;
的分布列;
(2)求 的数学期望;
的数学期望;
(3)求“所选3人中女生人数 ”的概率.
”的概率.
(本小题14分)设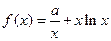 ,
, .
.
(1)当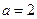 时,求曲线
时,求曲线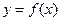 在
在 处的切线方程;
处的切线方程;
(2)如果存在 ,使得
,使得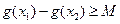 成立,
成立,
求满足上述条件的最大整数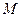 ;
;
(3)如果对任意的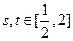 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题15分)已知椭圆 的右焦点恰好是抛物线
的右焦点恰好是抛物线 的焦点
的焦点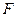 ,
,
点 是椭圆
是椭圆 的右顶点.过点
的右顶点.过点 的直线
的直线 交抛物线
交抛物线 于
于 两点,满足
两点,满足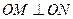 ,
,
其中 是坐标原点.
是坐标原点.
(1)求椭圆
 的方程;
的方程;
(2)过椭圆 的左顶点
的左顶点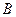 作
作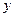 轴平行线
轴平行线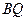 ,过点
,过点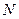 作
作 轴平行线
轴平行线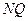 ,直线
,直线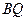 与
与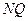 相交于点
相交于点 .若
.若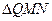 是以
是以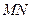 为一条腰的等腰三角形,求直线
为一条腰的等腰三角形,求直线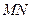 的方程.
的方程.