(本小题14分)设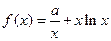 ,
,  .
.
(1)当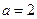 时,求曲线
时,求曲线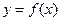 在
在 处的切线方程;
处的切线方程;
(2)如果存在 ,使得
,使得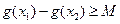 成立,
成立,
求满足上述条件的最大整数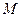 ;
;
(3)如果对任意的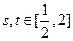 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
设平面向量 ,
,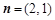 ,函数
,函数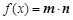 .
.
(1)当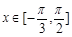 时,求函数
时,求函数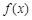 的取值范围;
的取值范围;
(2)当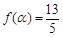 ,且
,且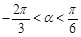 时,求
时,求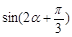 的值.
的值.
已知函数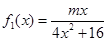 ,
,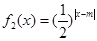 ,其中m∈R.
,其中m∈R.
(1)若0<m≤2,试判断函数f (x)=f1 (x)+f2 (x) 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(2)设函数 若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.
若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.
已知数列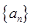 ,
, 满足
满足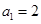 ,
,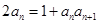 ,
,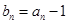 ,数列
,数列 的前
的前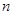 项和为
项和为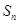 ,
,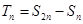 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求证: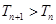 ;
;
(3)求证:当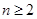 时,
时,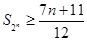 .
.
一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点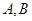 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
(1)若保持其缺口宽度不变,求裁剪后梯形缺口面积的最小值;
(2)若保持其缺口深度不变,求裁剪后梯形缺口面积的最小值.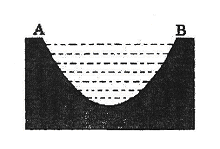
在平面直角坐标系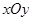 中,如图,已知椭圆E:
中,如图,已知椭圆E: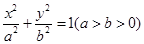 的左、右顶点分别为
的左、右顶点分别为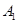 、
、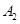 ,上、下顶点分别为
,上、下顶点分别为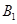 、
、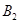 .设直线
.设直线 的倾斜角的正弦值为
的倾斜角的正弦值为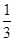 ,圆
,圆 与以线段
与以线段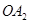 为直径的圆关于直线
为直径的圆关于直线 对称.
对称.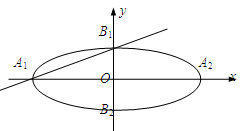
(1)求椭圆E的离心率;
(2)判断直线 与圆
与圆 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若圆 的面积为
的面积为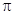 ,求圆
,求圆 的方程.
的方程.