如图,在四棱 锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。
锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。 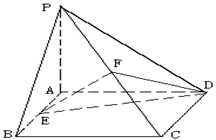
⑴求证:CD⊥PD;
⑵求证:EF∥平面PAD;
⑶若直线EF⊥平面PCD,求平面PCD与平面ABCD所成二面角的大小
选修4-1:几何证明选讲
如图所示,圆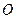 的直径
的直径 ,
, 为圆周上一点,
为圆周上一点, ,过
,过 作圆的切线
作圆的切线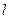 ,过
,过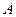 作
作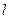 的垂线
的垂线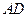 ,垂足为
,垂足为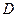 ,求∠DAC
,求∠DAC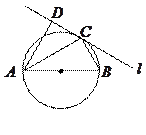
已知函数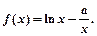
(1)若 在定义域内的单调性;
在定义域内的单调性;
(2)若 的值;
的值;
(3)若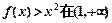 上恒成立,求a的取值范围.
上恒成立,求a的取值范围.
(本题满分12分)
已知函数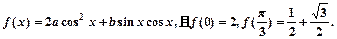
(1)求a,b的值;
(2)求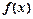 的最大值及取得最大值时x的集合;
的最大值及取得最大值时x的集合;
(3)写出函数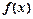 在[0,
在[0, ]上的单调递减区间.
]上的单调递减区间.
(某本题满分12分)
某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为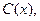 当年产量不足80千件时,
当年产量不足80千件时,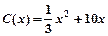 (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时, (万元).通过市场分析,若每件售价为500元时,该厂当年生产该产品能全部销售完.
(万元).通过市场分析,若每件售价为500元时,该厂当年生产该产品能全部销售完.
(1)写出年利润 (万元)关于年产量x(千件)的函数解析式;
(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一产品的生产中所获利润最大,最大利润是多少?
已知函数f(x)=ax3+bx+c (a>0)为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导数f/(x)的 最小值为-12,求a,b,c的值.