椭圆E的中心在原点O,焦点在x轴上,离心率e=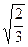 ,过点C(-1,0)的直线
,过点C(-1,0)的直线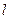 交椭圆于A,B两点,且满足
交椭圆于A,B两点,且满足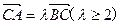 ,
, 为常数。
为常数。
(1)当直线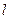 的斜率k=1且
的斜率k=1且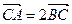 时,求三角形OAB的面积.
时,求三角形OAB的面积.
(2)当三角形OAB的面积取得最大值时,求椭圆E的方程.
(本小题满分12分)已知动圆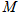 过定点
过定点 (0,1),且与
(0,1),且与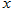 轴相切,点
轴相切,点 关于圆心
关于圆心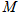 的对称点为
的对称点为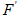 ,动点
,动点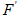 的轨迹为
的轨迹为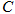 .
.
(1)求曲线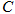 的方程;
的方程;
(2)设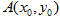 是曲线
是曲线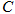 上的一个定点,过点
上的一个定点,过点 作两条倾斜角互补的直线,分别与曲线
作两条倾斜角互补的直线,分别与曲线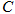 相交于另外两点
相交于另外两点 、
、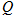 .证明直线
.证明直线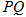 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.
(本小题满分12分)如图,在三棱柱 中,点
中,点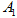 在侧面
在侧面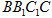 的射影为正方形
的射影为正方形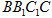 的中心M,且
的中心M,且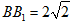 ,
,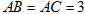 ,E为
,E为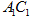 的中点.
的中点.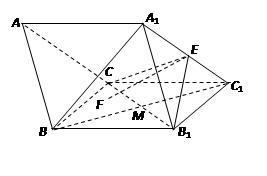
(1)求证: ║平面
║平面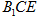 ;
;
(2)求二面角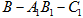 的正弦值;
的正弦值;
(3)在正方形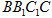 (包括边界)内是否存在点
(包括边界)内是否存在点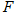 ,使得
,使得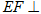 平面
平面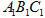 ?若存在,求出线段
?若存在,求出线段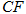 的长;若不存在,说明理由.
的长;若不存在,说明理由.
(本小题满分12分)已知圆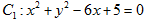 ,过圆
,过圆 上一点A(3,2)的动直线与圆
上一点A(3,2)的动直线与圆 相交于另一个不同的点B.
相交于另一个不同的点B.
(1)求线段AB的中点P的轨迹M的方程;
(2)若直线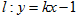 与曲线M只有一个交点,求
与曲线M只有一个交点,求 的值.
的值.
(本小题满分12分)如图,已知长方形 中,
中,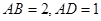 ,
,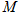 为
为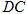 的中点.
的中点.
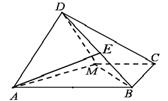
将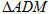 沿
沿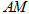 折起,使得平面
折起,使得平面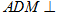 平面
平面 为
为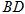 的中点.
的中点.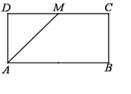
(1)求证: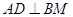 ;
;
(2)求直线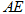 与平面ADM所成角的正弦值.
与平面ADM所成角的正弦值.
(本小题满分10分)设命题p:函数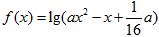 的定义域为R,
的定义域为R,
命题q:双曲线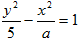 的离心率
的离心率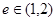 ,
,
(1)如果p是真命题,求实数 的取值范围;
的取值范围;
(2)如果命题“p或q”为真命题,且命题“p且q”为假命题,求实数 的取值范围.
的取值范围.