.从4名男生和2名女生中任选3人参加演讲比赛,设随机变量 表示所选3人中女生的人数.
表示所选3人中女生的人数.
(1)求 的分布列;
的分布列;
(2)求 的数学期望;
的数学期望;
(3)求“所选3人中女生人数 ”的概率.
”的概率.
在△ABC中,角A,B,C所对的边分别为a,b,c,且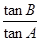 +1=
+1= .
.
(1)求B;
(2)若cos(C+ )=
)= ,求sinA的值.
,求sinA的值.
已知函数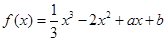 的图象在点
的图象在点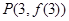 处的切线方程为
处的切线方程为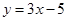 .
.
(1)求实数 的值;
的值;
(2)设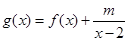 .
.
①若 是
是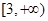 上的增函数,求实数
上的增函数,求实数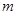 的最大值;
的最大值;
②是否存在点 ,使得过点
,使得过点 的直线若能与曲线
的直线若能与曲线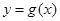 围成两个封闭图形,则这两个封闭图形的面积总相等.若存在,求出点
围成两个封闭图形,则这两个封闭图形的面积总相等.若存在,求出点 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
已知椭圆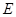 的两个焦点分别为
的两个焦点分别为 和
和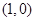 ,离心率
,离心率 .
.
(1)求椭圆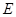 的方程;
的方程;
(2)若直线 (
(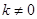 )与椭圆
)与椭圆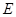 交于不同的两点
交于不同的两点 、
、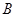 ,且线段
,且线段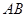
的垂直平分线过定点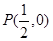 ,求实数
,求实数 的取值范围.
的取值范围.
已知数列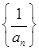 是公差为
是公差为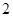 的等差数列,且
的等差数列,且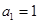 .
.
(1)求数列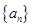 的通项公式;
的通项公式;
(2)设数列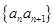 的前
的前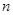 项和为
项和为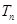 .
.
证明: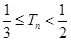 .
.
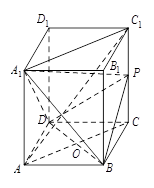
如图:已知长方体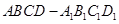 的底面
的底面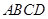 是边长为
是边长为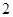 的正方形,高
的正方形,高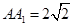 ,
,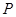 为
为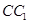 的中点,
的中点,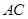 与
与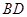 交于
交于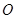 点.
点.
(1)求证: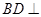 平面
平面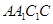 ;
;
(2)求证: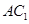 ∥平面
∥平面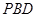 ;
;
(3)求三棱锥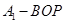 的体积.
的体积.