（本小题满分14分）如图，在直三棱柱
中，AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点
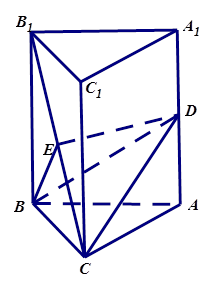
（1）求证：DE∥平面ABC；
（2）求三棱锥E-BCD的体积。
求中心在原点，对称轴为坐标轴，一个焦点是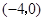
，一条渐近线是
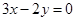的双曲线方程及离心率．
已知椭圆的焦点是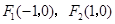
，
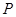为椭圆上一点，且
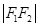是
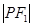和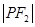
的等差中项．
（1）求椭圆的方程；
（2）若点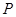在第三象限，且
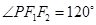，求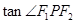
．
已知大西北某荒漠上A、B两点相距2km，现准备在荒漠上开垦出一片以AB为一条对角线的平行四边形区域建成农艺园，按照规划，围墙总长为8km，问农艺园的最大面积能达到多少？
设
分别为椭圆
的左、右两个焦点．
（1）若椭圆
上的点
到两点的距离之和等于4，写出椭圆的方程和焦点坐标；
（2）设点
是（1）中所得椭圆上的动点，求线段
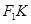的中点的轨迹方程．
在平面直角坐标系中，已知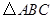
的两个顶点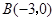
，
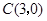且三边AC、BC、AB的长成等差数列，求顶点A的轨迹方程．