函数 的图象如下图所示.
的图象如下图所示.
(1)求解析式中 的值;
的值; 
(2)该图像可由 的图像先向_____(填“左”或“右”)平移_______个单位,
的图像先向_____(填“左”或“右”)平移_______个单位,
再横向拉伸到原来的_______倍.纵向拉伸到原来的______倍得到.
(本小题满分12分)设 是定义在
是定义在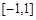 上的奇函数,函数
上的奇函数,函数 与
与 的图象关于
的图象关于 轴对称,且当
轴对称,且当 时,
时, .
.
(1)求函数 的解析式;
的解析式;
(2)若对于区间 上任意的
上任意的 ,都有
,都有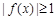 成立,求实数
成立,求实数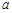 的取值范围.
的取值范围.
如图,O为坐标原点,点F为抛物线C1: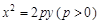 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2: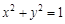 相切于点Q.
相切于点Q.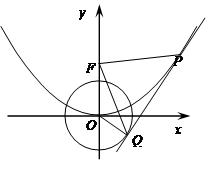
(Ⅰ)当直线PQ的方程为 时,求抛物线C1的方程;
时,求抛物线C1的方程;
(Ⅱ)当正数 变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求
变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求 的最小值.
的最小值.
(本小题满分12分)如图甲,⊙ 的直径
的直径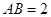 ,圆上两点
,圆上两点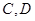 在直径
在直径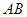 的两侧,使
的两侧,使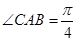 ,
,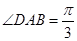 .沿直径
.沿直径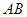 折起,使两个半圆所在的平面互相垂直(如图乙),
折起,使两个半圆所在的平面互相垂直(如图乙),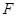 为
为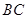 的中点,
的中点,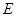 为
为 的中点.
的中点. 为
为 上的动点,根据图乙解答下列各题:
上的动点,根据图乙解答下列各题: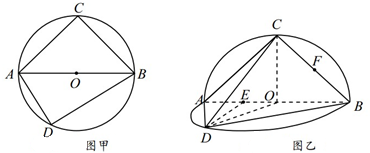
(1)求点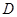 到平面
到平面 的距离;
的距离;
(2)在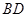 弧上是否存在一点
弧上是否存在一点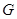 ,使得
,使得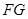 ∥平面
∥平面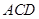 ?若存在,试确定点
?若存在,试确定点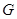 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(本小题满分12分)已知函数 (
( 、
、 为常数).
为常数).
(1)若 ,解不等式
,解不等式 ;
;
(2)若 ,当
,当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)如图,在平面直角坐标系 中,点
中,点 在单位圆
在单位圆 上,
上, ,且
,且 .
.
(1)若 ,求
,求 的值;
的值;
(2)若 也是单位圆
也是单位圆 上的点,且
上的点,且 .过点
.过点 分别做
分别做 轴的垂线,垂足为
轴的垂线,垂足为 ,记
,记 的面积为
的面积为 ,
, 的面积为
的面积为 .设
.设 ,求函数
,求函数 的最大值.
的最大值.