（1）求证：平面EFG∥平面CB1D1；
（2）求证：平面CAA1C1⊥平面CB1D1 ；
（3）求异面直线FG、B1C所成的角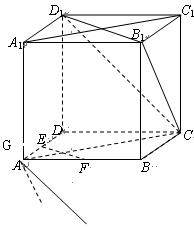
（本小题满分10分）△ABC中，内角A，B，C的对边分别为a，b，c，已知a，b，c成等比数列，
（Ⅰ）求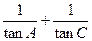
的值；（Ⅱ）设
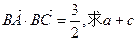的值
（本小题满分10分）已知数列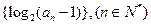
为等差数列，且
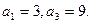（１）求数列
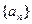的通项公式；(2)求数列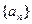的前n项和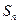
(本小题满分14分)
己知函数
，(Ⅰ)证明函数
是R上的增函数；
(Ⅱ)求函数的值域．(Ⅲ)令
．判定函数
的奇偶性，并证明
（本小题13分）
测量地震级别的里氏是地震强度（即地震释放的能量）的常用对数值，显然级别越高，地震的强度也越高。如日本1923年地震为8.9级，旧金山1906年地震是8.3级，1989年地震为7.1级。试计算一下日本1923年地震强度是8.3级的几倍？是7.1级的几倍？（取lg2=0.3）
已知函数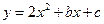
在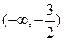
上是减函数，在
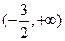上是增函数，且两个零点
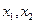满足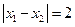
，求二次函数的解析式。