设函数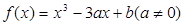
(1)若曲线 在点
在点 处的切线方程是
处的切线方程是 ,求
,求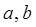 的值
的值
(2)求函数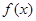 的单调区间及极值
的单调区间及极值
已知椭圆C: 的左焦点
的左焦点 坐标为
坐标为 ,且椭圆C的短轴长为4,斜率为1的直线
,且椭圆C的短轴长为4,斜率为1的直线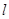 与椭圆G交于A,B两点,以AB为底边的等腰三角形,顶点为
与椭圆G交于A,B两点,以AB为底边的等腰三角形,顶点为 .
.
(1)求椭圆C的方程
(2)求 的面积
的面积
已知等比数列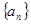 满足,
满足,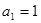 ,
,
(1)求数列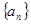 的通项公式
的通项公式
(2)若等差数列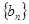 的前n项和为
的前n项和为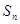 ,满足
,满足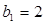 ,
,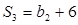 ,求数列
,求数列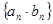 的前n项和
的前n项和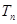
设函数 ,若
,若 在
在 处有极值
处有极值
(1)求实数 的值
的值
(2)求函数 的极值
的极值
(3)若对任意的
 ,都有
,都有 ,求实数
,求实数 的取值范围
的取值范围
分别求适合下列条件的圆锥曲线的标准方程:
(1)离心率为 ,焦点坐标为
,焦点坐标为 和
和 的双曲线
的双曲线
(2)离心率 ,准线方程为
,准线方程为 的椭圆
的椭圆
(3)焦点在 轴的正半轴上,焦点到准线的距离为4的抛物线
轴的正半轴上,焦点到准线的距离为4的抛物线