已知双曲线 1的右焦点是
1的右焦点是 ,右顶点是
,右顶点是 ,虚轴的上端点是
,虚轴的上端点是 ,
, ,
, .
.
(1)求该双曲线的方程;
(2)设 是双曲线上的一点,且过点
是双曲线上的一点,且过点 、
、 的直线
的直线 与
与 轴交于点
轴交于点 ,若
,若 求直线
求直线 的斜率.
的斜率.
(本小题满分13分)
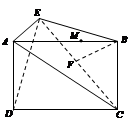
如图,四边形 为矩形,
为矩形,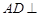 平面
平面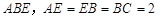 ,
,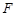 为
为 上的点,且
上的点,且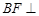 平面
平面 .
.
(1)求证: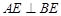 ;
;
(2)求三棱锥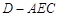 的体积;
的体积;
(3)设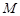 在线段
在线段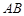 上,且满足
上,且满足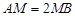 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得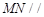 平面
平面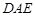 .
.
(本小题满分12分)
设函数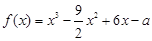 .
.
(1)对于任意实数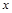 ,
,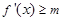 在
在 恒成立(其中
恒成立(其中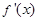 表示
表示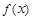 的导函数),求
的导函数),求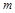 的最大值;
的最大值;
(2)若方程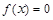 在
在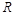 上有且仅有一个实根,求
上有且仅有一个实根,求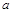 的取值范围.
的取值范围.
(本小题满分12分)
在“2012魅力新安江”青少年才艺表演评比活动中,参赛选手成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下图,据此回答以下问题:
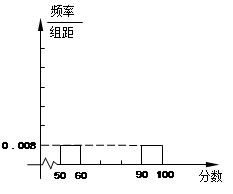
(1)求参赛总人数和频率分布直方图中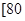 ,
,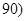 之间的矩形的高,并完成直方图;
之间的矩形的高,并完成直方图;
(2)若要从分数在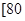 ,
,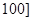 之间任取两份进行分析,在抽取的结果中,求至少有一份分数在
之间任取两份进行分析,在抽取的结果中,求至少有一份分数在 ,
,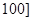 之间的概率.
之间的概率.
(本小题满分12分)
已知 为
为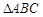 的三内角,且其对边分别为
的三内角,且其对边分别为 .若向量
.若向量 ,
, ,向量
,向量 ,
,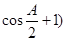 ,且
,且 .
.
(1)求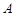 的值; (2)若
的值; (2)若 ,三角形面积
,三角形面积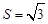 ,求
,求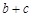 的值.
的值.
(本小题满分10分)已知函数 为偶函数,且在
为偶函数,且在 上为增函数.
上为增函数.
(1)求 的值,并确定
的值,并确定 的解析式;
的解析式;
(2)若 且
且 ,是否存在实数
,是否存在实数 使
使 在区间
在区间 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.