(理)袋中有同样的球 个,其中
个,其中 个红色,
个红色, 个黄色,现从中随机且不返回地摸球,每次摸
个黄色,现从中随机且不返回地摸球,每次摸 个,当两种颜色的球都被摸到时,即停止摸球,记随机变量
个,当两种颜色的球都被摸到时,即停止摸球,记随机变量 为此时已摸球的次数,求:.
为此时已摸球的次数,求:.
(1)随机变量 的概率分布律;
的概率分布律;
(2)随机变量 的数学期望与方差.
的数学期望与方差.
(12分)已知数列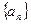 满足
满足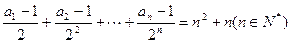 .
.
(1)求数列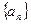 的通项公式. (2)求数列
的通项公式. (2)求数列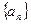 前
前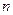 项和
项和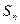 .
.
(12)如图,四棱锥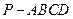 的底面
的底面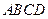 为正方形,
为正方形,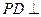 平面
平面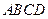 ,
,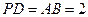 ,
,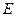
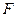 ,
,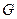 分别为
分别为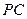 ,
,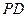 和
和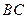 的中点. (1)求证
的中点. (1)求证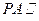 平面
平面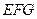 .(2)求异面直线
.(2)求异面直线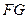 与
与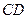 所成角的正切值.
所成角的正切值.
(12分)已知函数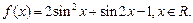
(1)求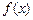 的最小正周期及
的最小正周期及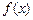 取得最大值时x的集合.
取得最大值时x的集合.
(2)在平面直角坐标系中画出函数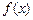 在
在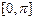 上的图象(在图上标明关键点的坐标)
上的图象(在图上标明关键点的坐标)
设函数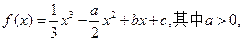 曲线
曲线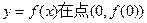 处的切线方程为y=1。
处的切线方程为y=1。
(1)确定b,c的值。
(2)若过点(0,2)能且只能作曲线y=f(x)的一条切线,求a的取值范围。
已知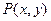 为函数
为函数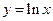 图象上一点,
图象上一点,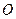 为坐标原点.记直线
为坐标原点.记直线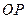 的斜率
的斜率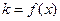 。
。
(1)同学甲发现:点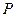 从左向右运动时,
从左向右运动时,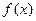 不断增大,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的判断。
不断增大,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的判断。
(2)同学乙发现:总存在正实数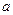 、
、 ,使
,使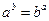 .试问:他的判断是否正确?若不正确,请说明理由:若正确,请求出
.试问:他的判断是否正确?若不正确,请说明理由:若正确,请求出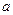 的取值范围。
的取值范围。